【cg】【pbr】基于物理的渲染实现篇之直接光照

发表于 更新于 分类于 阅读次数： 本文字数： 5.8k 阅读时长 ≈ 5 分钟

前言

上篇介绍了PBR的一些理论基础，本篇基于这些理论，并选择了一个典型的Cook-Torrance BRDF模型，来尝试实现一下精准光源直接光照的计算，其中所引用到的上节的公式先列于此，以便后面引用。

\[ L(p, \vec{v}) = \int_{\vec{l}_i \in \Omega} f(p, \vec{l}_i, \vec{v}) \ast L(p, \vec{l}_i) \ast (\vec{n} \cdot \vec{l}_{i}) \ast d\vec{l}_i \tag{0.19} \]

\[ f_{lambert} (p, \vec{l}, \vec{v}) = k_d \ast \frac {C_{diffuse}} {\pi} \tag{0.22} \]

\[ f_{cook\_torrance}(p, \vec{l}, \vec{v}) = \frac {D(p, \vec{h}) \ast G(p, \vec{l}, \vec{v}) \ast F(p, \vec{l}, \vec{v})} {4 \ast (\vec{n} \cdot \vec{v}) \ast (\vec{n} \cdot \vec{l})} \tag{0.23} \]

精准光源

所谓精准光源，是指当某个点被其照亮时，这个点只会被来自一个方向的一条光线照亮，区别于面积光源、体积光源，常见的精准光源有如平行光、点光源、聚光等。

而我们这里所说的直接光照，便是这些精准光源对平面的直接照射光线，而非通过反射再照射到平面的光线。由于平面上的每个点都只会有一条光线照射进来，所以我们最后的光照强度并不需要在半球领域进行积分, 即最终的颜色值只是一次反射率方程计算的结果，这也是本篇最终要实现的目的。

BRDF项

这里使用的还是上篇介绍的Cook-Torrance BRDF模型框架，分漫反射项和镜面反射项两部分进行论述，其中镜面反射项分别选用具体的DGF模型来实现BRDF项。

漫反射项

漫反射项使用的是Cook-Torrance BRDF模型的漫反射部分，即公式\((0.22)\)。

其中\(k_d\)为漫反射项的能量守恒系数，在后面讨论能量守恒再详细分析。

镜面反射项

镜面反射项同样使用的是上篇介绍的Cook-Torrance BRDF模型的镜面反射部分，即公式\((0.23)\)。

正如上篇所述，其中法线分布函数D和几何函数G都是基于统计学的估算模型，即前人在大量物理测量的基础上，通过建模、显微镜观测表面分布几何外形、寻找与物理事实相近的函数模型等，并基于此进行归纳计算等操作得来的。而菲涅尔方程F也是通过Fresnel-Schlick方程求得的近似解。下面分别来看。

法线分布函数

法线分布函数是基于测量数据库进行的统计学建模，其中效果比较好的也是Disney、UE4及大部分厂商使用的法线分布函数为Trowbridge和Reit于1975年公布的GGX模型，简称tr_ggx，其公式如下。

\[ D_{tr\_ggx} (p, \vec{n}, \vec{h}) = \frac {\alpha^2} {\pi * ((\vec{n} \cdot \vec{h})^2 * (\alpha^2 - 1) + 1)^2} \tag{1.1} \]

其函数图像如图所示。

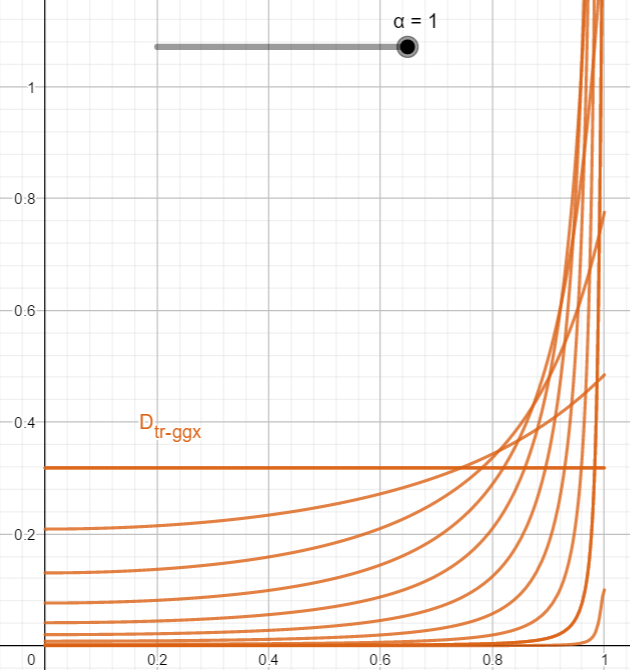
法线分布函数

可以看到，中间向量\(\vec{h}\)越接近平面的法线\(\vec{n}\)，D函数的值越大，可反射光到人眼的微表面越多，从而形成高光区域，同时拥有更好的高光长尾。

图中\(\alpha\)为粗糙度，也可以看出，粗糙度越高，函数越平缓，其高光区域越大，而高光强度越低。这也与我们之前论述的结论相一致。

除此之外，Disney发现若\(\alpha\)为粗糙度的平方，函数曲线会更平滑，可得到更好的光照效果，这也称为Disney法则，即

\[ \alpha = roughness^2 \tag{1.2} \]

最终tr_ggx法线分布函数的glsl实现如下。

1
2
3
4
5
6
7
8
float brdf_d_tr_ggx(float n_o_h, float roughness) {
    float a = roughness * roughness;
    float a2 = a * a;

    float x = a2;
    float y = (n_o_h*n_o_h * (a2-1.0) + 1.0);
    return x / max(pi * y * y, 0.001);
}

几何函数

与D函数类似的，G函数也是基于测量数据库进行的统计学建模。这里使用的是Schlick-GGX几何遮蔽函数，其公式如下

\[ G_{schlick\_ggx} (p, \vec{n}, \vec{v}) = \frac {\vec{n} \cdot \vec{v}} {(\vec{n} \cdot \vec{v}) * (1 - k) + k} \tag{1.3} \]

其中

\[ k = \frac {\alpha} {2} \tag{1.4} \]

图像如下。

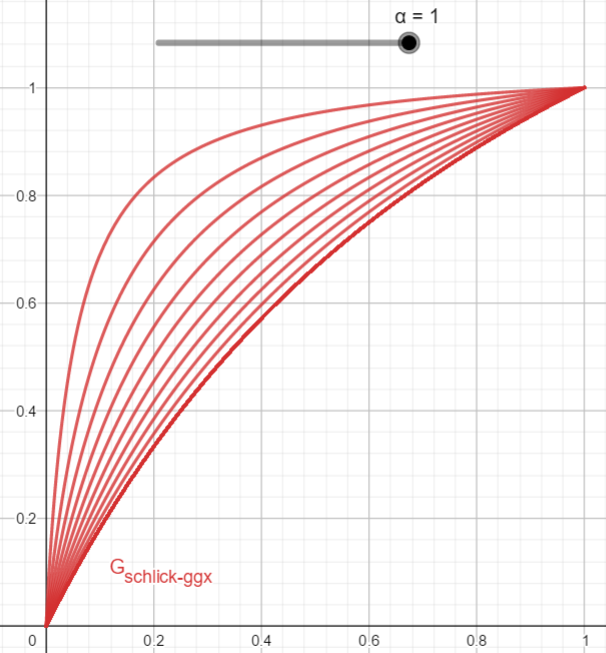
几何分布函数

\((1.4)\)是为了对粗糙度进行重新映射，以得到更符合现实的效果。然而这里的\(\alpha\)的含义与\((1.2)\)却不相同。这里针对直接光照进行了新的重映射，即

\[ \alpha = \frac {roughness + 1} {2} \tag{1.5} \]

即将roughness的[0.0,1.0]线性映射到了[0.5,1.0]，产生了更平缓的曲线。

除此之外，\((5-3)\)只考虑了几何遮蔽，并没有考虑几何阴影。但是如果我们将表示观察方向的参数\(\vec{v}\)改为表示入射方向的参数\(\vec{l}\)，那么\((5-3)\)就可以表示为几何阴影函数了。

最终的G项需要既考虑几何遮蔽，又要考虑几何阴影，所以可以将这两个方程结合起来获得，当然这种结合方式是多种多样的，这里使用ue4使用的分离遮蔽阴影模型(smith模型)，即将两个部分直接乘起来，这也是最简单的组合方式，即

\[ G_{smith\_ggx} (p, \vec{n}, \vec{l}, \vec{v}) = G_{schlick\_ggx} (p, \vec{n}, \vec{l}) * G_{schlick\_ggx} (p, \vec{n}, \vec{v}) \tag{1.6} \]

其最终的glsl代码实现如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
float brdf_g_k_direct(float roughness) {
    // k = alpha / 2
    // alpha = (roughness + 1) / 2
    return (roughness + 1.0)*(roughness + 1.0) / 8.0;
}
float brdf_g_schlick_ggx(float n_o_v, float k) {
    float x = n_o_v;
    float y = n_o_v * (1.0 - k) + k;
    return x / max(y, 0.001);
}
float brdf_g_smith(float n_o_v, float n_o_l, float k) {
    float g_v = brdf_g_schlick_ggx(n_o_v, k);
    float g_l = brdf_g_schlick_ggx(n_o_l, k);

    return g_v * g_l;
}

菲涅尔方程

菲涅尔方程本身的推导和使用本人还未曾研究过，这里采用的是Schlick近似方程。

\[ F_{schlick} (p, \vec{l}, \vec{v}) = F_0 + (1 - F_0) * (1 - (\vec{n} \cdot \vec{v}))^5 \tag{1.7} \]

这里\(F_0\)是基础反射率，是我们从与法线\(\vec{n}\)垂直90度的角度观察平面时的反射率，它是使用折射指数(IOR)计算得来的。

这里的\(F_0\)及\((1.7)\)是对于电介质等非金属而言的，而对于金属，是通过预计算出入射光线为法线时的\(F_0\)，然后再根据金属度，对表面反射率albedo和\(F_0\)进行插值得到的。即

\[ f_{0\_m} = metallic * albedo + (1 - metallic) * F_0 \tag{1.8} \]

除此之外，对于微平面来说，使用宏观法线\(\vec{n}\)是不准确的，所以我们将其改为微观法线(即中间向量)\(\vec{h}\)。即

\[ F_{schlick} (p, \vec{l}, \vec{v}) = F_0 + (1 - F_0) * (1 - (\vec{h} \cdot \vec{v}))^5 \tag{1.9} \]

最后也给出F函数的glsl代码。

1
2
3
4
5
6
7
vec3  brdf_f_f0(vec3 f0, vec3 albedo, float metallic) {
    return mix(f0, albedo, metallic);
    // return metallic * albedo + (1.0 - metallic) * f0;
}
vec3 brdf_f_schlick(float h_o_v, vec3 f0) {
    return f0 + (1.0 - f0) * pow(1.0 - h_o_v, 5.0);
}

金属度与能量守恒系数

由能量守恒和可知

\[ f(p, \vec{l}, \vec{v}) = k_d * f_{lambert}(p, \vec{l}, \vec{v}) + k_s * f_{cook\_torrance}(p, \vec{l}, \vec{v}) \tag{1.10} \]

这里的\(k_d\)和\(k_s\)分别是漫反射项和镜面反射项的比例系数。

由上篇理论可知，菲涅尔方程就是反射的光线占总光线的比例，也就是镜面反射项的比例，即\(k_s = F\)，所以\(k_s\)已经被算到\(f_{cook\\_torrance}\)里了，这里不用再加入此系数。

那么对于\(k_d\)，如果所有的折射光最终都反射出来，那么显然有\(k_d=(1-k_s)\)。

这对于非金属来说可能成立。但是对于金属来说，其金属度越高，则对折射光的吸收能力越强，所以作如下调整。

\[ k_d = (1.0 - k_s) * (1.0 - metallic) \tag{1.11} \]

当金属度为1.0的时候，\(k_d\)为0，不会折射光线出去，也就没有漫反射项。符合物理现象。

最后，给出基于上述结论实现的整个Cook-Torrance BRDF模型的glsl代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
vec3 brdf_cook_torrance(vec3 n, vec3 v, vec3 l,
                        vec3 c_diffuse, vec3 c_specular,
                        vec3 f0, float roughness, float metallic) {
    // pre cac
    vec3 h = normalize(v + l);                          // 中间向量
    float n_o_v = max(dot(n, v), 0.0);
    float n_o_l = max(dot(n, l), 0.0);
    float n_o_h = max(dot(n, h), 0.0);
    float h_o_v = max(dot(h, v), 0.0);

    // D函数
    float d = brdf_d_tr_ggx(n_o_h, roughness);          // 法线分布函数

    // G函数
    float k = brdf_g_k_direct(roughness);               // k值映射 -- 用于计算G函数
    float g = brdf_g_smith(n_o_v, n_o_l, k);            // 几何函数

    // F函数
    vec3 f90 = brdf_f_f0(f0, c_specular, metallic);     // 获取真正的 f0_m -- 有金属性影响
    vec3 f = brdf_f_fresnel_schlick(h_o_v, f90);        // 菲涅尔方程

    // 能量守恒系数
    vec3 k_s = f;                                       // 镜面反射系数 -- 等于菲涅尔方程的值
    vec3 k_d = (vec3(1.0) - k_s) * (1.0 - metallic);    // 漫反射系数 -- 考虑金属度

    // 最终代入公式计算
    vec3 diffuse = c_diffuse / pi;
    vec3 x = d * g * f;
    float y = max(4.0 * n_o_v * n_o_l, 0.001);
    vec3 speculr = x / y;

    return k_d * diffuse + /*k_s */ speculr;            // 不需要 k_s -- 已经有菲涅尔系数了
}

反射率方程

正如本篇一开始所说，这里计算的是精准光源的直接光照，所以不需要积分，那么根据公式\((0.19)\)，可知现在的直接光照结果为

\[ L(p, \vec{l}, \vec{v}) = f_{brdf}(p, \vec{l}, \vec{v}) * radiance * (\vec{n} \cdot \vec{l}) \tag{1.12} \]

对应的glsl代码如下。

1
2
3
4
5
6
7
8
9
10
vec3 pbr_Lo(vec3 n, vec3 v, vec3 l,
            vec3 c_diffuse, vec3 c_specular,
            vec3 f0, float roughness, float metallic,
            vec3 radiance) {

    float n_o_l = max(dot(n, l), 0.0);
    vec3 brdf = brdf_cook_torrance(n, v, l, c_diffuse, c_specular, f0, roughness, metallic);

    return brdf * radiance * n_o_l;
}

结语

最终的实现效果如下图所示。图为只有一个平行光时的情况。

pbr直接光照结果
pbr直接光照结果

本章将上章的理论应用于实际，实现了对PBR光照模型的直接光照的计算。

其中法线分布函数使用GGX模型，几何函数使用Schlick-GGX模型结合分离遮蔽阴影函数，菲涅尔方程使用Schlick近似。

由于进行直接光照的光源属于精准光源，所以并不需要在半球领域积分。

整个光照计算的过程中，传入了粗糙度(roughness)和金属度(metallic)两个重要参数。同时还有表示基础反射率的常量\(F_0\)以及表面反光度(通常为镜面反射颜色)(albedo)。

下篇将继续探索和实现基于IBL(Image Based Lighting)的间接光照，包括Brute force的IBL方案和Epic的IBL方案。

\(o)/