【cg】【球谐光照】球谐函数
前言
本篇我们来继续研究球谐函数的解及其性质。上回书说到求解拉普拉斯方程的结果着落在了伴随勒让德多项式上,本文我们首先会先接着上文的结论讨论一下伴随勒让德多项式的一相特性,必最终解出球谐函数的具体表达式。然后接着类比傅立叶变换研究一下球谐函数的投影和重建过程。最后讨论球谐函数的两个重要性质,即正交完备性与旋转不变性。
本文需要用到的在上回书中提到的公式列举如下。
\[ \left\{ \begin{array}{l} x = r\sin\theta \cos\varphi \\ y = r\sin\theta \sin\varphi \\ z = r\cos\theta \end{array} \right. \tag{2.3} \]
\[ \varPhi(\varphi) = e^{im\varphi}, m \in Z \tag{3.11} \]
\[ \frac{\mathrm{d}}{\mathrm{d} x} [ (1-x^2) \frac{\mathrm{d} y}{\mathrm{d} x} ] + [ l(l+1) - \frac{m^2}{1-x^2} ] y = 0 \tag{3.12} \]
\[ \Theta(\theta) = P_l^m(\cos\theta),l \in N, m \in Z, |m| \leq l \tag{3.13} \]
伴随勒让德多项式
上文中\((3.12)\)便是伴随勒让德方程,它的解构成的伴随勒让德多项式,其解析式如下。
\[ P_l^m(x) = \frac{(-1)^m(1-x^2)^{\frac{m}{2}}}{2^l l!} \frac{\mathrm{d}^{l+m}}{\mathrm{d} x^{l+m}} [(x^2 - 1)^l] \tag{4.1} \]
求解方法
我们在编写程序求解时一般不直接套用\((4.1)\)这个公式,而是使用时间复杂度更低的递推关系来求出所有\(l、m\)取值内的\(P_l^m(x)\)值。其递推关系如下。
\[ \left\{ \begin{array}{l} P_m^m(x) = (-1)^m (2m-1)!! (1-x^2)^{\frac{m}{2}} \\ P_{m+1}^m = x(2m + 1) P_m^m(x) \\ (l-m) P_l^m(x) = x(2l-1) P_{l-1}^m - (l+m-1) P_{l-2}^m(x) \end{array} \right. \tag{4.2} \]
对于任意固定的m值,我们都可以求出所有的l(\(\geq m\))时的P值。
勒让德多项式
当\(m = 0\)时,伴随勒让德方程退化为勒让德方程。
\[ \frac{\mathrm{d}}{\mathrm{d} x} [ (1-x^2) \frac{\mathrm{d} y}{\mathrm{d} x} ] + l(l+1) y = 0 \tag{4.3} \]
其解也退化为勒让德多项式。
\[ P_l(x) = \frac{1}{2^l l!} \frac{\mathrm{d}^{l}}{\mathrm{d} x^{l}} [(x^2 - 1)^l] \tag{4.4} \]
该多项式不包含导数的表达式如下。
\[ P_l(x) = \frac{1}{2^l l!} \sum_{s=0}^{\lfloor \frac{1}{2} \rfloor} \frac{(-1)^s (2l-2s)!}{s! (l-s)! (l-2s)!} x^{l-2s} \tag{4.5} \]
我们可以通过这个表达式求出具体的多项式表达,下面列出前几项
\[ \left\{ \begin{array}{l} P_0(x) = 1 \\ P_1(x) = x \\ P_2(x) = \frac{1}{2}(3x^2 -1) \\ P_3(x) = \frac{1}{2}(5x^3 -3x) \\ \end{array} \right. \tag{4.6} \]
其与伴随勒让德多项式之间的关系为
\[ P_l^m(x) = (-1)^m (1-x^2)^{\frac{m}{2}} \frac{\mathrm{d}^m}{\mathrm{d} x^m} [P_l(x)] \tag{4.7} \]
可以看出伴随勒让德多项式其实是勒让德多项式的m阶导。
正交性
伴随勒让德多项式有一个重要的性质是它满足正交性。
\[ \int_{-1}^{1} P_l^m(x) P_k^n(x) \mathrm{d}x = \frac{(l+|m|)!}{(l-|m|)!} \frac{2}{2l + 1} \delta_{lk} \delta_{mn} \tag{4.7} \]
其中
\[ \delta_{lk} = \left\{ \begin{array}{l} 0, & l \neq k \\ 1, & l = k \end{array} \right. \]
意思是说任意相同两项之积在定义域内的积分结果为一个只与\(l、m\)相关的常数,任意不同两项之积在定义域内的积分结果为0。
这便是伴随勒让德多项式的正交性,这个性质相当重要。
球谐函数
球谐函数[4]是上面拉普拉斯方程解的角度部分,即\(Y(\theta, \varphi)\)。因为对于每一个确定的\(l、m\),都有一个解Y,记为\(Y_l^m(\theta, \varphi)\)。
由上面的结果\((3.11)(3.13)\)可得球谐函数的表达式如下。其中\(i\)为虚数单位,显然这是一个复数域的表达式。
\[ Y_l^m(\theta, \varphi) = (-1)^m N \Theta(\theta) \varPhi(\varphi) = (-1)^m N_l^m P_t^m(\cos\theta) e^{im\varphi} \]
其中\((-1)^m\)为Condon–Shortley相位,经常出现在物理学定义中,暂时可以忽略。
其中\(N_l^m = \sqrt{\frac{2l+1}{4\pi} \frac{(l - |m|)!}{(l + |m|)!}}\)为归一化因子,这个归一化与正交完备性有关。
正交完备性
由于\(P_l^m(x)\)是满足正交性的,如公式\((4.6)\)所示,所以我们只需要添加一个系数,就可以使球谐函数也满足正交性,且为正交完备(标准正交)的,即满足
\[ \int_S Y_l^m(\theta, \varphi) Y_k^n(\theta, \varphi) d\omega = \delta_{lk} \delta_{mn} \tag{5.0} \]
其中\(\omega\)为一个立体角方向,它与一组\(\theta、\varphi\)对应,即\(\omega \Leftrightarrow (\theta, \varphi)\)。
所以为了满足正交完备性而即归一化后的球谐函数为
\[ Y_l^m(\theta, \varphi) = (-1)^m \sqrt{\frac{2l+1}{4\pi} \frac{(l - |m|)!}{(l + |m|)!}} P_t^m(\cos\theta) e^{im\varphi} \tag{5.1} \]
实数形式
我们需要将上述复数形式转换为实数形式进行应用。当\(m > 0\)时,我们使用\(e^{im\varphi}\)的实部\(\cos(m\varphi)\),当\(m < 0\)时,我们使用其虚部\(\sin(-m\varphi)\),并调整规一化因子,可得其实数形式的表达式为
\[ Y_l^m(\theta, \varphi) = \left\{ \begin{array}{l} \sqrt{2} N_l^m P_l^m(\cos\theta) \cos(m\varphi) & m > 0 \\ \sqrt{2} N_l^m P_l^{-m}(\cos\theta) \sin(-m\varphi) & m < 0 \\ N_l^0 P_l^0(\cos\theta) & m = 0 \end{array} \right. \tag{5.2} \]
根据表达式\((5.2)\),我们尝试求出前三阶的所有的解,如下表所示。
| l m | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| 0 | \(\frac{1}{2} \sqrt{\frac{1}{\pi}}\) | ||||
| 1 | \(-\frac{1}{2} \sqrt{\frac{3}{\pi}} \sin\theta\sin\varphi\) | \(\frac{1}{2} \sqrt{\frac{3}{\pi}} \cos\theta\) | \(-\frac{1}{2} \sqrt{\frac{3}{\pi}} \sin\theta\cos\varphi\) | ||
| 2 | \(\frac{1}{4} \sqrt{\frac{15}{\pi}} \sin^2\theta\sin2\varphi\) | -\(\frac{1}{2} \sqrt{\frac{15}{\pi}} \sin\theta\cos\theta\sin\varphi\) | \(\frac{1}{4} \sqrt{\frac{5}{\pi}} (3\cos^2\theta -1)\) | -\(\frac{1}{2} \sqrt{\frac{15}{\pi}} \sin\theta\cos\theta\cos\varphi\) | \(\frac{1}{4} \sqrt{\frac{15}{\pi}} \sin^2\theta\cos2\varphi\) |
由\((2.3)\),易得当\(r=1\)时直角坐标系下的所有解,如下所示。
| l m | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| 0 | \(\frac{1}{2} \sqrt{\frac{1}{\pi}}\) \(\approx 0.282095\) | ||||
| 1 | \(-\frac{1}{2} \sqrt{\frac{3}{\pi}} y\) \(\approx -0.488603 y\) | \(\frac{1}{2} \sqrt{\frac{3}{\pi}} z\) \(\approx 0.488603 z\) | \(-\frac{1}{2} \sqrt{\frac{3}{\pi}} x\) \(\approx -0.488603 x\) | ||
| 2 | \(\frac{1}{2} \sqrt{\frac{15}{\pi}} xy\) \(\approx\) \(1.092548 xy\) | -\(\frac{1}{2} \sqrt{\frac{15}{\pi}} zy\) \(\approx\) \(-1.092548 zy\) | \(\frac{1}{4} \sqrt{\frac{5}{\pi}} (3z^2 -1)\) \(\approx\) \(0.315392 (3z^2-1)\) | -\(\frac{1}{2} \sqrt{\frac{15}{\pi}} zx\) \(\approx\) \(-1.092548 zx\) | \(\frac{1}{4} \sqrt{\frac{15}{\pi}} (x^2-y^2)\) \(\approx\) \(0.546274 (x^2-y^2)\) |
对比ue4自带的球谐函数代码,可以看到与我们自己计算的结果是一致的。
1 |
|
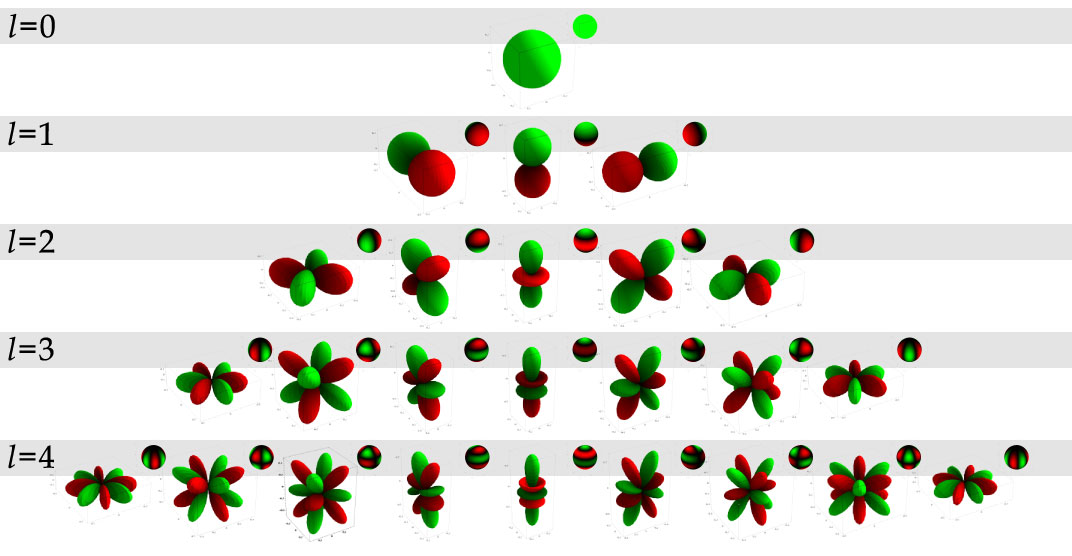
球谐函数的可视化图像如下。其中大图像是将球谐函数的值作为半径得到的,而右上角的小图像是固定半径为1,将球谐函数的值作为颜色值得到的。
投影与重建
我们在傅立叶变换[5]里有讨论过,任意满足条件的周期函数都可以通过三角函数系的原始轴(由不同频率正余弦组成)展开成傅立叶级数,即展开成一项项这些原始轴作为基底函数、目标函数在基底函数上的投影作为该基底函数项的系数的表达式。
类比到球谐函数上来,因为球谐函数是正交完备的,所以每一个球谐函数都可以作为基底函数,即作为原始轴,形成一个希尔伯特空间。那么对于任意目标函数,我们是否也可以像傅立叶级数展开那样,使用这以球谐函数作为基底函数来展开呢?如果可以展开,那么如何确定目标函数在基底函数上的投影(即系数)呢?
我们采用求傅立叶级数类似的方法,先假设可以展开,然后再寻找系数的表达式。
为了使后续的描述和公式更优雅,我们首先将\(Y_l^m\)由二维序列展平成一维序列。设\(k = l(l+1) + m\),记\(b_k = Y_l^m\),那么对于给定的阶数L,总共有\(n = L^2\)个球谐函数,即
\[ \{b_0, b_1, b_2, b_3, b_4, \ldots, b_{n-1}\} \Leftrightarrow \{Y_0^0, Y_1^{-1}, Y_1^0, Y_1^1, Y_2^{-2}, \ldots, Y_{L-1}^{L-1}\} \]
设目标函数为\(f(\theta, \varphi)\),假设其可以由以下级数展开。
\[ f(\theta, \varphi) = \sum_{k=0}^{k<n} c_k \cdot b_k \tag{5.3} \]
其中\(c_k\)即为基底函数\(b_k\)对应的系数,也是目标函数\(f\)在该基底函数上的投影。
下面我们来确定系数\(c_k\)。确定系数其实是一个拟合问题,即我们需要找出这样的系数,使得展开后的函数更接近原函数。
这种问题我们可以使用最小二乘法来解决,即寻找这样的系数,使得拟合后的函数与目标函数的方差最小。设方差为\(E\),则有
\[ E = \int_S (\sum_{k=0}^{k<n} c_k \cdot b_k - f)^2 d\omega \tag{5.4} \]
我们来求公式\((5.4)\)的最小值。对任意\(k \in [0, n)\),\((5.4)\)可以看作是关于\(c_k\)的二次方程,所以其关于\(c_k\)的导数为0,即
\[ \begin{array}{l} \frac{\mathrm{d} E}{\mathrm{d} c_k} &=& 2 \int\limits_S (\sum\limits_{i=0}^{i<n} c_i \cdot b_i - f) b_k d\omega \\ &=& 2 \int\limits_S (\sum\limits_{i=0}^{i<n} c_i b_i b_k) d\omega - 2 \int_S\limits f \cdot b_k d\omega \\ &=& 2 \sum\limits_{i=0}^{i<n} c_i \int\limits_S b_i b_k d\omega - 2 \int\limits_S f \cdot b_k d\omega \\ &=& 2 \sum\limits_{i=0}^{i<n} c_i \delta_{ik} - 2 \int\limits_S f \cdot b_k d\omega \\ &=& 2 c_k - 2 \int\limits_S f \cdot b_k d\omega = 0\\ \end{array} \]
所以有
\[ c_k = \int_S f(\theta, \varphi) \cdot b_k(\theta, \varphi) d\omega \tag{5.5} \]
即基底函数\(b_k\)对应的系数,是该基底函数与目标函数的乘积在定义域上的定积分。
显然公式右侧为目标函数\(f\)与基底函数的内积,一般记作\(\langle f, b_k\rangle\)。巧合的是,我们求傅立叶级数的系数的时候,最终得到的结果也是三角函数系与目标函数的内积。
至此,我们会发现,将目标函数使用球谐函数作为基底展开,与使用傅立叶级数展开,其系数都是希尔伯特空间下的内积,可以说其本质几乎没有差别,只不过将三角函数系换成了球谐函数系,这也许就是我们谈到球谐函数时总会提及傅立叶变换相关内容的原因了。
上述由目标函数得到各基底的系数的过程称作投影,如公式\((5.5)\)。而从系数生成级数拟合出原函数的过程称作重建,如公式\((5.3)\)。
旋转不变性
球谐函数的另一个重要的性质就是旋转不变性。
设\(\omega\)为一个立体角方向,它与一组\(\theta、\varphi\)对应,即\(\omega \Leftrightarrow (\theta, \varphi)\)。
设\(R^{(\alpha, \beta, \gamma)}(\omega)\)表示将\(\omega\)按\((\alpha, \beta, \gamma)\)欧拉角进行旋转。
设原函数为\(f(\omega)\),我们可以对其使用球谐函数展开,其球谐系数如\((5.5)\)所示,即有
\[ f(\omega) = \sum_l^n\sum_{m = -l}^{m = l} c_l^m \cdot Y_l^m(\omega) \tag{5.6} \]
我们对原函数进行该旋转操作,得到旋转后的函数\(f(R^{(\alpha, \beta, \gamma)}(\omega))\),即有
\[ f(R^{(\alpha, \beta, \gamma)}(\omega)) = \sum_l^n\sum_{m = -l}^{m = l} c_l^m \cdot Y_l^m(R^{(\alpha, \beta, \gamma)}(\omega)) \tag{5.7} \]
若旋转后的函数仍使用原来的球谐函数进行展开,则便需要新的球谐系数,设为\(C_l^k\),即需要有
\[ f(R^{(\alpha, \beta, \gamma)}(\omega)) = \sum_l^n\sum_{m = -l}^{m = l} C_l^m \cdot Y_l^m(\omega) \tag{5.8} \]
其中球谐系数为
\[ C_l^m = \int_S f(R^{(\alpha, \beta, \gamma)}(\omega)) Y_l^m(\omega) \mathbb{d} \omega \tag{5.9} \]
可以看出,当我们对原函数进行旋转时,我们需要重新在球面上进行积分来求得球谐系数,这个性能开销是极高的。
而球谐函数的旋转不变性是说,我们并不需要重新求得旋转后的球谐函数及其系数,我们可以通过原球谐函数的线性组合表示出旋转后的球谐函数,也可以通过原系数的线性组合表示出旋转后的系数。这就省略了积分部分。
旋转后的球谐函数可使用原球谐函数的线性组合表示,如下所示。
\[ Y_l^m(R^{(\alpha, \beta, \gamma)}(\omega)) = \sum_{m' = -l}^{m' = l} D_{m', m}^l(\alpha, \beta, \gamma) \cdot Y_l^{m'}(\omega) \tag{5.10} \]
其中
\[ D_{m', m}^l(\alpha, \beta, \gamma) = e^{-im'\alpha} \cdot d_{m', m}^l(\beta) \cdot e^{-im\gamma} \tag{5.11} \]
其中\(D_{m', m}^l(\alpha, \beta, \gamma)\)为魏格纳D矩阵(Wigner D-matrix)[6]。这是群论里的概念,它是SO(3)广义转动群的同构群,即SO(3)广义转动群的不可约表示的酉矩阵(共轨转置=逆)。
其中\(d_{m', m}^l(\beta) = D_{m', m}^l(0, \beta, 0)\)为魏格纳d矩阵,它是D矩阵的一种特殊情况。
我们暂时可以不必理解这个魏格纳D矩阵,只需要知道对于已知的\((\alpha, \beta, \gamma)\),它可以确定一个维度为\((2l+1)\)的方阵,该方阵中每一个元素的值仅由\((l、m、\alpha、\beta、\gamma)\)确定。
我们将\((5.10)(5.11)\)代入到\((5.7)\),可得
\[ \begin{array}{l} f(R^{(\alpha, \beta, \gamma)}(\omega)) &=& \sum\limits_l^n\sum\limits_{m = -l}^{m = l} c_l^m \cdot \sum\limits_{m' = -l}^{m' = l} D_{m', m}^l(\alpha, \beta, \gamma) \cdot Y_l^{m'}(\omega) \\ &=& \sum\limits_l^n \sum\limits_{m' = -l}^{m' = l} \underbrace{\sum\limits_{m = -l}^{m = l} c_l^m \cdot D_{m', m}^l(\alpha, \beta, \gamma)}_{C_l^{m'}} \cdot Y_l^{m'}(\omega) \\ &=& \sum\limits_l^n \sum\limits_{m' = -l}^{m' = l} C_l^{m'} \cdot Y_l^{m'}(\omega) \end{array} \tag{5.12} \]
其中新的球谐系数为
\[ C_l^{m'} = \sum\limits_{m = -l}^{m = l} c_l^m \cdot D_{m', m}^l(\alpha, \beta, \gamma) \tag{5.13} \]
对于确定的旋转\((\alpha, \beta, \gamma)\),由\((l、m)\)决定下标的D矩阵的每个元素,都可以求出其具体值,所以上式表明,新的球谐系数可以由旧的球谐系数的线性组合来获得,而不用再次求积分,这就是球谐函数的旋转不变性。
后记
关于球谐函数的投影与重建的应用,我们会在下一篇关于PRT的文章中使用到。
关于球谐函数的旋转不变性,本节只简述了下原理和结论,关于其应用部分我们会在下一篇关于PRT的文章中使用到。而关于其严谨且复杂的证明过程,此处先挖个坑埋个土,后续会另开一篇文章详细讨论一下,此处不作赘述。