【cg】【原理】光照模型
前言
常见的基本光照模型 (illumination model)
Phong Lighting Model — 冯氏光照模型
Blinn-Phone -- 布林-冯氏光照模型
Lambert -- 兰伯特光照模型
Rendering Equation -- 全局光照模型 (渲染方程)
预备知识
RGB 颜色模型
颜色的数字化表示 -- RGB -- 红 (Red) 绿 (Green) 蓝 (Blue) -- (R, G, B)
一个 vector3 (3维向量) 就可以表示一种颜色 -- 每一个分量的范围 [0.0, 1.0] 表示强度
我们现实中看到的物体的颜色并非其真正的颜色, 而是它反射(Reflected)的 颜色
一个物体会吸收(Absorb) 与它本身颜色不同的颜色, 而它拒绝吸收的颜色即为我们看到的颜色
如一个蓝色的物体会吸收除了蓝色以外的其他颜色, 不能被吸收的蓝色才会反射到我们眼中
如果光源本身是有颜色的, 你想像一下, 用一个发蓝色光的手电筒去照一个红色的物体, 会看到什么呢? 可以肯定的是它不会变成奥特曼, 但是这却是一个我们必须搞清楚的问题

我们假设光源(手电筒)的颜色为 light_color , 物体的颜色为 object_color
简单起见, 我们先从太阳光 (白光) 开始研究, 假设此时 light_color = (1.0, 1.0, 1.0), 再假设此时 object_color = (1.0, 0.5, 0.3)
如果我们把这两个值相乘, 会得到什么呢
1 | result_color = light_color * object_color; |
我们发现物体反射的颜色就是它原本的颜色, 这也符合现实, 毕竟白色的光照的确实是物体本身的颜色
我们再来试个不用白光的例子, 白光太平凡了

假设 light_color = (0.0, 0.0, 1.0) 即蓝光, object_color 保持不变, 那么
1 | result_color = light_color * object_color = (0.0, 0.0, 0.3); |
最后的颜色完全没有了红色和绿色的成分, 而且只反射了 0.3 的蓝光
到了这里, 是不是可以这样理解, 光源的颜色就像是原料, 而物体的颜色则是工具。
即物体的颜色决定反射各个颜色分量的强度
如上面的 0.3 表示这个物体会反射光源 30% 的蓝色光, 由于光源的蓝色光原料为 100% , 那么最后反射到我们眼睛里的颜色就是 0.3 的蓝色光了。
怎么样, 是不是很有道理的样子 ?

最后, 我们就可以来对物体的颜色重新下个定义 :
物体的颜色 是 物体能反射一个光源的各个颜色分量的强度 (大小)
光源类型
光源又可以叫投光物(light caster) , 因为它们要把颜色源料投射到物体上嘛
但是不同类型的光源会有不同的效果, 其自身也有一些特有的类型 (衰减, 平滑什么的)。
根据光源的 位置 和 方向 及其他特性可以将光源分为以下几种基本类型。
环境光 Ambient Light
先给一个比较专业的定义 :
没有位置, 没有方向, 且对场景中的__所有物体__ 都有相同的效果的光
环境光来源于光线可以在任何物体上反射, 那此不被太阳光直接照射的物体也会将间接反射到他们身上的光再次反射出去
所以说在这个世界上, 几乎没有物体是完全黑暗的 (除了人的心hhhh)

平行光 Directional Light
没有位置 (也可以说在无限远处) , 只有固定的方向, 所以对场景中的所有物体都有相同的方向
一个最好的例子就是 太阳光 , 太阳光足够远到我们可以把它视为无限远
所以来自太阳的光线就类似于平行光线了
点光源 Point Light
有固定位置, 朝所有方向发光, 但是光线会随着距离逐渐衰减
这个比较好理解, 相像一下灯泡, 火把啊什么的, 就明白了
衰减
随着光线传播距离的增长, 光的强度会被逐渐地减弱, 这种现象通常叫 衰减 (Attenuation)
至于随着具体的衰减方式, 则可以通过一个 以距离为参数 的方程来定义了
比较常用的衰减方程是
\[ I_{att}(d) = \frac{1.0}{k_c + k_l * d + k_q * d^2} \tag{1.1} \]
其中 \(d\) 即为与光源的距离
\(k_c\) \(k_l\) \(k_q\) 分别为常数项, 一次项, 二次项的系数
整个方程其实就是一个一元二次方程的倒数
由于这些系数通过为正数, 所以整个方程是一个单调递减的
这样做的实际意义是, 距离近的时候光源的强度会下降的非常快, 而距离远了之后剩下的光强就会下降的非常慢了, 比较符合现实世界的情况
而对于参数的取值, 又有另外的经验问题需要讨论

常数项通常保持为 1.0, 用来保证分母永远不会比 1.0 小
一次项可表示以线性的方式减少光的强度
二次项可表示以二次递减的方式减少光的强度
也就是说, 随着距离的增大, 二次项会在某个位置超过一次项, 此时衰减速度会非常快, 到了后面由于光强慢慢变少, 就是以更慢的速度逐渐衰减, 直到慢慢变为 0
下面这张图片 (来自 learnopengl) 可以说明实际的衰减情况 (横轴表示距离, 纵轴表示当前的光强)
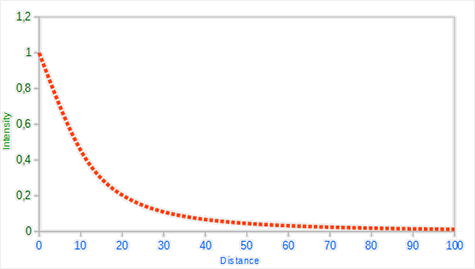
那么关于参数的取值, 就会直接影响到最后的衰减效果了, 而且最后的取值会取决于很多因素
所以这就涉及到一个经验问题了, 下面是 Wiki 上提供的经验数据
| 距离 | 常数项 | 一次项 | 二次项 |
|---|---|---|---|
| 7 | 1.0 | 0.7 | 1.8 |
| 13 | 1.0 | 0.35 | 0.44 |
| 20 | 1.0 | 0.22 | 0.20 |
| 32 | 1.0 | 0.14 | 0.07 |
| 50 | 1.0 | 0.09 | 0.032 |
| 65 | 1.0 | 0.07 | 0.017 |
| 100 | 1.0 | 0.045 | 0.0075 |
| 160 | 1.0 | 0.027 | 0.0028 |
| 200 | 1.0 | 0.022 | 0.0019 |
| 325 | 1.0 | 0.014 | 0.0007 |
| 600 | 1.0 | 0.007 | 0.0002 |
| 3250 | 1.0 | 0.0014 | 0.000007 |
可以看到所有的常数项都是 1.0, 一次项都很小, 这是为了覆盖更远的距离, 二次项更小
聚光灯 Spot Light
有固定位置, 朝特定的方向发光
与点光的最大区别就是点光源朝所有的方向都发光
让我们来看看要想打造一个聚光效果, 都需要哪些东西
light_position -- 聚光源在世界空间的位置
spot_direction -- 聚光源的方向向量 -- 一般指正前方的方向
\(\phi\) (phi) -- 内切光角 (inner cutoff angle) -- 聚光源可以发光的内边界与 spot_direction 之间的夹角
\(\gamma\) (gamma) -- 外切光角 (outer cutoff angle) -- 聚光源可以发光的外边界与 spot_direction 之间的夹角
而对于一个物体来说, 要想计算它所能反射的聚光灯的强度, 还需要知道的是
light_direction -- 从物体到光源的方向向量
\(\theta\) (theta) -- light_direction 与 spot_direction 之间的夹角
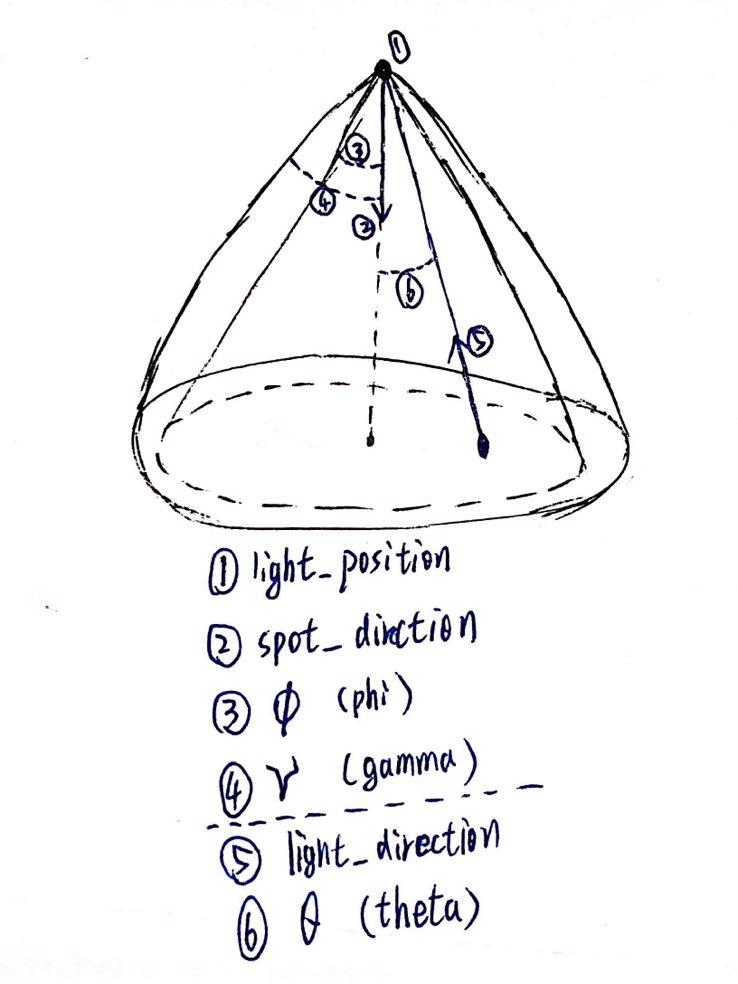
下面我们来分情况讨论一下, 物体在各个位置的光照情况
当物体在内切角以内的时候
\[ \theta<\phi \Rightarrow cos(\theta)>cos(\phi) \]
聚光灯的光照强度系数 (对光照强度的影响) 为 1
当物体在内切角与外切角之间的时候
\[ \phi<\theta<\gamma \Rightarrow cos(\gamma) < cos(\theta) < cos(\phi) \]
聚光灯的光照强度系数 (对光照强度的影响) 为 \(\frac{cos(\theta)-cos(\gamma)}{cos(\phi)-cos(\gamma)}\)
这是一个插值
当物体在外切角以外的时候
\[ \theta > \gamma \Rightarrow cos(\theta) < cos(\gamma) \]
聚光灯的光照强度系数 (对光照强度的影响) 为 0
最后我们有一个完整的公式 \(I_{spot}(\theta)\) 来表示聚光灯的强度系数
\[ I_{spot} (\theta) = \begin{cases} 1, & \text{if $ \theta < \phi $ } & \text{ $ cos(\theta) > cos(\phi) $ } \\ \frac{cos(\theta) - cos(\gamma)}{cos(\phi) - cos(\gamma)}, & \text{if $ \phi < \theta < \gamma $ } & \text{ $ cos(\gamma) < cos(\theta) < cos(\phi) $ } \\ 0, & \text{if $ \theta > \gamma $ } & \text{ $ cos(\theta) < cos(\gamma) $ } \end{cases} \]
Lambert -- 兰伯特光照模型
Lambert 光照模型是一种理想的__漫反射__模型
漫反射 (diffuse reflection) 是粗糙的物体表面向各个方向等强度地反射光的现象
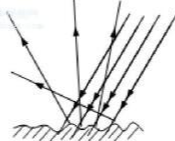
它不包含任何镜面属性
对于粗糙的物体, 可以体现出一种 磨砂效果
那么为什么说它是 理想 的呢 ?
事实上, 粗糙表面向各个方向反射光的强度都是不同的,
而 理想 的状态是其朝各个方向反射光的强度都是相同的
能产生这种效果的反射体称为 理想漫反射体 , 也称 兰伯特反射体
至于其具体的定义和细节, 为了以后可方便扩充, 这里就另启一篇来写了, 后面的其他光照模型也是如此
Phong Lighting Model -- 冯氏光照模型
Blinn-Phone -- 布林-冯氏光照模型
PBR (Physically Based Rendering) -- 基于物理的渲染
本篇词汇表
illumination model -- 光照模型
rendering equation -- 渲染方程
light caster -- 投光物
ambient light -- 环境光
directional light -- 平行光 (定向光)
point light -- 点光
spot light -- 聚光
attenuation -- 衰减
intensity -- 强度/亮度
diffuse reflection -- 漫反射
注意
light -- 光; lighting -- 光照 (与 illumination 同)