关于brdf的两件小事
前言
某日午时小憩,与某巨佬闲聊,谈及关于brdf的两个问题,发现从前虽有涉猎,但未求甚解,甚为惭愧,掩面而去。。今痛定思痛,翻阅典籍,重新推演,豁然开朗,但觉从未有如此刻般了然,遂记于此,聊以为物外之趣。
问题1:brdf的单位是什么?为什么?
答:球面度(立体角)分之一(\(\frac{1}{sr}\))。
要想解答这个问题,不得不先弄清楚brdf的定义及其物理意义。
什么是brdf
brdf(双向反射分布函数, bidirectional reflective distribution function), 是指当一束光从某个方向(\(\vec{l}\))照射到某个点(p)上时,在某个方向上(\(\vec{v}\))的出射辐射通量占总的入射辐射通量的比例。
所以如果对于点p来说,brdf是一个函数的话,那么它便有两个自变量,即光源的入射方向\(\vec{l}\)和某个观察方向\(\vec{v}\),我们将它记为
\[ f(\vec{l}, \vec{v}) \]
如果我们设出射辐射通量为\(P_{out}\),入射辐射通量为\(P_{in}\)的话,那么就有
\[ f(\vec{l}, \vec{v}) = \frac{P_{out}}{P_{in}} \tag{1.1} \]
首先来看一张图,图中单位半球表示其圆心p的半球领域。绿色的圆锥对应从\(\vec{l}\)方向入射的光锥所对应的立体角。蓝色的圆锥对应向\(\vec{v}\)方向出射的光锥所对应的立体角。橙色的圆锥表示从其他方向入射的光线。可以将橙色圆锥们认定为半球领域上分别从四面八方所有方向上入射的光线。
那么brdf便是图中从p点出射的蓝色圆锥占进入p点的绿色圆锥的比例。

下面我们分别来看分母和分子部分。
分母部分
我们知道,入射光的辐射照度\(E_{in}\)是半球领域所有方向上的辐射通量,即对应上图中所有的绿色和橙色的圆锥。
所以这里的分母便是\(E_{in}\)在入射方向\(\vec{l}\)上的微分,其微元为入射方向的立体角\(d\vec{l}\)。对应图中绿色的圆锥部分。即
\[ P_{in} = dE_{in}(\vec{l}) \tag{1.2} \]
我们知道,辐射照度是指在单位表面积上的辐射通量,其单位是瓦特每平方米(\(W/m^2\)),显然,其微分\(dE_{in}(\vec{l})\)的单位也是瓦特每平方米。
关于上句话里的显然,可以进一步解释一下。微分\(dE\)是对于微元\(d\vec{l}\)的微分,是对于某个极小的立体角的微分,所以它还是单位立体角的值 * 立体角这种形式。单位立体角的辐射照度,其实就是辐射亮度,即类似下面这种格式。
\[ 辐射照度E = 辐射亮度L * 立体角\Omega \]
其实根据辐射照度和辐射亮度的定义,有如下公式,以前证过,此处不做额外证明。
\[ dE_{in}(\vec{l}) = L(\vec{l}) \cos{\theta} \cdot{d\omega} \tag{1.3} \]
从这个公式中也可以看出来其单位为
\[ \frac{W}{m^2 \cdot{sr} } \cdot{ sr } = \frac{W}{m^2} \]
可以类比路程=速度*时间,对于微元为时间的路程微分,其单位也还是长度单位。
\[ S = v * t, (m = m/s * s) \] \[ dS = v * dt, (m = m/s * s) \]
所以,分母部分的单位是瓦特每平方米(\(W/m^2\))。
分子部分
如果光源的入射方向并非\(\vec{l}\),而是从整个半球领域四面八方而来(如上图中所有绿色和橙色的圆锥)的话,那么从观察方向\(\vec{v}\)出射的辐射通量便正好是在\(\vec{v}\)方向的辐射亮度\(L(\vec{v})\),即在观察方向\(\vec{v}\)上的单位表面积单位立体角对应的辐射通量,其单位是瓦特每平方米每球面度(\(W/(m^2 * sr)\))。
但是,光源的入射方向并非四面八方,而是仅从入射方向\(\vec{l}\)入射,即上图绿色的圆锥,那么最终的出射的辐射通量自然也大打折扣,变成了原来的辐射亮度\(L(\vec{v})\)在入射方向\(\vec{l}\)上的微分,即
\[ P_{out} = dL(\vec{v}) \tag{1.4} \]
需要注意,微分\(dL(\vec{v})\)的微元也是\(d\vec{l}\),而非\(d\vec{v}\)。
因为辐射亮度\(L(\vec{v})\)的单位是瓦特每平方米每球面度(\(W/m^2 * sr\)),那么其微分\(dL(\vec{v})\)的单位也是如此。
所以分子部分的单位是瓦特每平方米每球面度(\(W/(m^2 * sr)\))。
真正的原因
由上面的分析可得,最终brdf的公式为
\[ brdf = f(\vec{l}, \vec{v}) = \frac{dL(\vec{v})}{dE_{in}(\vec{l})} \tag{1.5} \]
而其单位为
\[ \frac{\frac{W}{m^2 \cdot{sr} }}{\frac{W}{m^2}} = \frac{1}{sr} \]
一顿猛如虎的操作之后,我们似乎解答了这个问题\^o^/,看起来还顺便理解了brdf的定义,感觉很完美,但事情上却并非如此-_-||。
事情上,有一个很关键的问题被我们忽略了,那就是,我们为什么非得要对入射方向\(\vec{l}\)微分?我们为什么要求入射方向上的极小微元\(d\vec{l}\)?我们直接求入射方向上的单位立体角\(\Omega\)不好吗?
也就是说,在上面的推导过程中,我们始终认为绿色的圆锥的底面积是无穷小,即整个半球领域可以划分成无穷多个绿色的圆锥。但是如果绿色的圆锥的底面积是1,即整个半球领域可以划分成\(2\pi\)个绿色的圆锥的时候,我们同样也可以进行上面的过程。
好!我们来求求试试,假设正好有一束光沿\(\vec{l}\)照射到p点,其立体角正好是单位立体角,那么
入射辐射通量就是\(\vec{l}\)方向上的辐射亮度,即
\[ P_{in} = L(\vec{l})\cos{\theta} \tag{1.6} \]
对于出射辐射通量,我们前面刚刚说过,如果光源的入射方向来自整个半球领域四面八方,那么出射辐射通量为\(L(\vec{v})\),此时立体角的值为\(2\pi\),那么入射方向只有1立体角时有
\[ P_{out} = \frac{L(\vec{v})}{2\pi} \tag{1.7} \]
此时brdf为
\[ brdf = f(\vec{l}, \vec{v}) = \frac{L(\vec{v})}{2\pi\cos\theta \cdot{L(\vec{l})}} \tag{1.8} \]
此时brdf的单位为1,貌似也可以啊!!
所以问题来了,brdf为什么不按照上面的方式定义呢,单位为1,公式好记,利好广大深受其害的人民群众。
其实这跟光的测量有关,我们知道真正被广泛使用的brdf模型,都是通过测量来得到的拟合公式,如著名的cook-torrance brdf,所以能够测量brdf的值是很有必要的。
当科学家们使用测量仪测量辐射亮度和辐射照度的时候,受限于光源的形状,很难使入射光源刚好填充1立体角,但是却可以使用一个极小的光源填充为某一个微元方向(如\(\vec{l}\))上的立体角,从而测量出入射方向上的辐射照度微分,以及出射方向上的辐射亮度微分。
即如果按照我们一开始对入射方向\(\vec{l}\)微分的方式定义brdf,那么科学家们只需要使用一个极小的光源从\(\vec{l}\)方向入射到点p,就可以测得brdf的值。但是如果按照第二种方式,就很难输入一个填充立体角刚好等于1的光源。
个人认为,将入射方向上的无穷小\(d\vec{l}\)作为微元,是导致brdf的单位为\(1/sr\)的根本原因。
而之所以将入射方向上的无穷小\(d\vec{l}\)作为微元,是因为这是一种使测量可以实施的方案,而填充1立体角无法实施。
问题2:lambert漫反射的brdf是什么?为什么?
答:\(\frac{1}{\pi}\)。
lambert漫反射的意思是,当一束光入射到某点p上时,其向任意方向出射的光照强度都是相等的。而对于其光照强度的计算遵循lambert定律,即其光照强度与入射方向\(\vec{l}\)和表面法线\(\vec{n}\)的夹角的余弦成正比,即对半球领域上的任意出射方向\(\vec{v}\),都有
\[ L(\vec{v}) = C_{diffuse} \cdot (\vec{l}\cdot\vec{n}) \tag{2.1} \]
其中\(C_{diffuse}\)是p点表面的漫反射贴图颜色。显示上述公式是一种经验模型,不是基于物理的,是不符合能量守恒的。
那么如果我们想使其在满足定义的前提下,同样符合能量守恒的话,是怎么样的呢。
同样参照上面的动图,现在我们假设p点是一个遵循lambert漫反射的理想漫反射体。绿色的圆锥为从\(\vec{l}\)方向入射的一条漫反射光线,蓝色的圆锥为向\(\vec{v}\)方向出射的光线,那么根据上一个问题我们对brdf的分析,目前这种情况是一模一样的,同样满足公式\((1.5)\),所以我们可以得到在出射方向\(\vec{v}\)上的辐射亮度为
\[ dL(\vec{v}) = f(\vec{l}, \vec{v}) \cdot dE_{in}(\vec{l}) \tag{2.2} \]
同前面一样的道理,因为入射的光源是一个在\(\vec{l}\)上的微元,所以这个公式是一个微元为\(d\vec{l}\)的微分辐射亮度。那么如果入射光是来自整个半球领域四面八方的话(如图中所有的绿色和橙色圆锥),那么从\(\vec{v}\)出射的辐射亮度便是微分\((2.2)\)在半球领域的积分了,如下所示
\[ L(\vec{v}) = \int_{\vec{l}_i \in \Omega} dL(\vec{v}) = \int_{\vec{l}_i \in \Omega} f(\vec{l}_i, \vec{v}) \cdot dE_{in}(\vec{l_i}) \tag{2.3} \]
由前文提到的公式\((1.3)\),可以将\(dE_{in}(\vec{l})\)进一步展开,使用出射方向的辐射亮度来表示,那么公式\((2.3)\)最终可化为
\[ L(\vec{v}) = \int_{\vec{l}_i \in \Omega} f(\vec{l_i}, \vec{v}) \cdot L(\vec{l}_i) \cos{\theta} \cdot d\vec{l}_i \tag{2.4} \]
等下,公式\((2.4)\)好生眼熟,,这不就是渲染方程吗(-_-其实是反射率方程,减化了折射和散射部分的渲染方程,这里就叫渲染方程好了)。
ok,我承认我们的推导过程有些跑偏,一个不小心走了一遍渲染方程的推导,,方程\((1.3)(1.5)(2.2)(2.3)(2.4)\)便是从brdf的定义开始到得到渲染方程的近乎全部过程了。不过没关系,我们马上回到对lambert的brdf的推导上来。
回到正轨
正文开始。-_-||
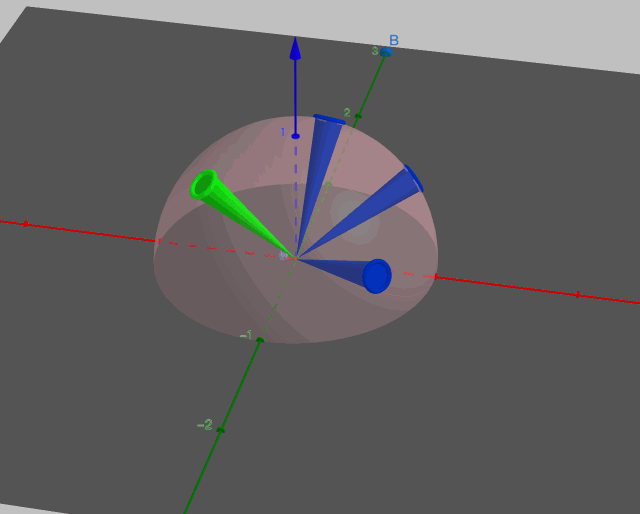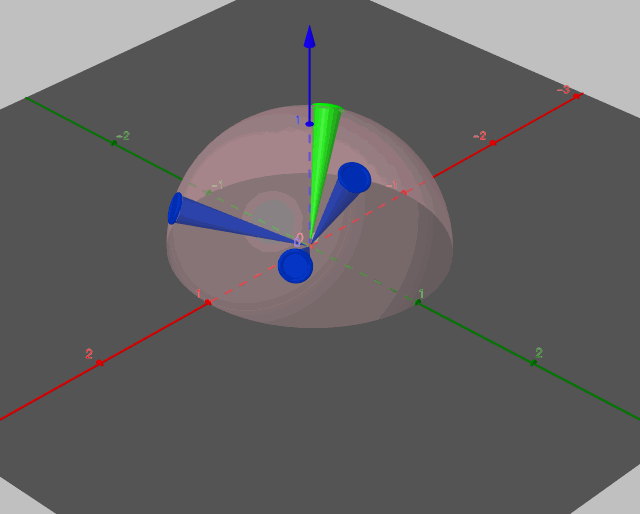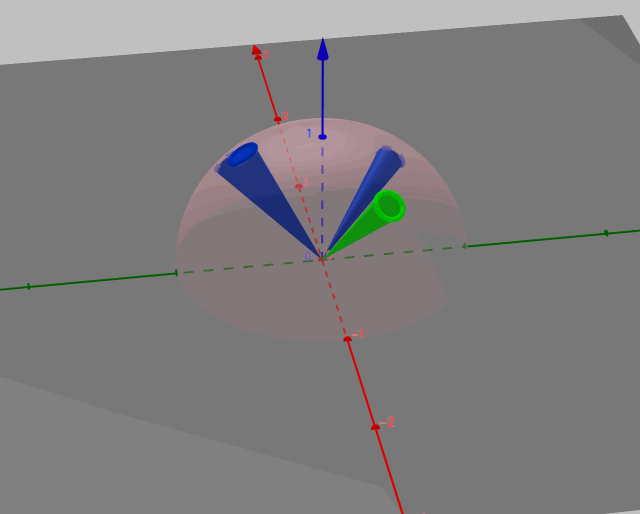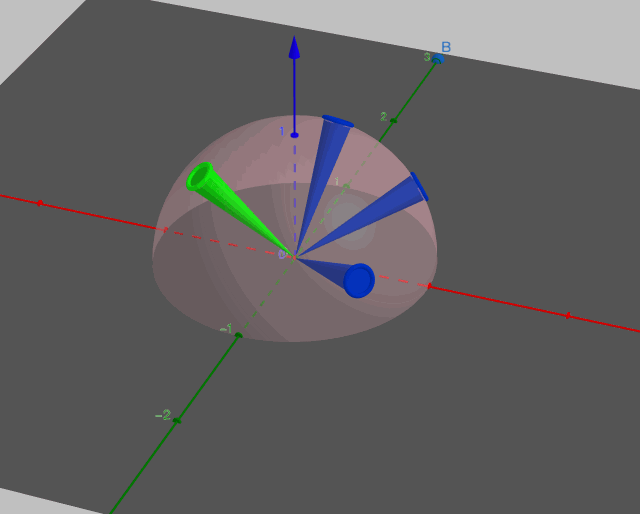
如图所示,一束立体角为无穷小的光线沿入射方向\(\vec{l}\)照射到点p上,即图中的绿色圆锥。遵循lambert漫反射,它会向半球领域上的任意出射方向\(\vec{v}_i\)射出立体角为无穷小的光线,如图中所有的蓝色圆锥,此时半球领域可以切分成无穷多个这样的蓝色圆锥。
下面我们分别来看入射辐射通量和出射辐射通量分别是什么。
入射辐射通量
显然此时入射辐射通量是入射方向上的微分辐射照度,即
\[ P_{in} = dE_{in}(\vec{l}) \tag{3.1} \]
出射辐射通量
此时从任意出射方向\(\vec{v}_i\)出射的辐射通量,显然都是在那个方向上的微分辐射照度,即
\[ dP_{out}(\vec{v}_i) = dE_{out}(\vec{v}_i) \tag{3.2} \]
又由辐射照度和辐射亮度的定义,即公式\((1.3)\),辐射照度可以用辐射亮度来表示,那么上述公式可表示为如下公式。其中\(L(\vec{v}_i)\)为\(\vec{v}_i\)方向上的辐射亮度(入射辐射通量为\(\vec{l}\)方向上的时),\(\theta\)为点p法线方向与\(\vec{v}_i\)的夹角,\(d\vec{v}_i\)为\(\vec{v}\)方向上的无穷小的微元立体角。
\[ dP_{out}(\vec{v}_i) = L(\vec{v}_i)\cos{\theta} \cdot d\vec{v}_i \tag{3.3} \]
那么总的出射辐射通量即为上述微分在半球领域上的积分,即
\[ P_{out} = \int_{\vec{v}_i \in \Omega} dP_{out}(\vec{v}_i) = \int_{\vec{v}_i \in \Omega} L(\vec{v}_i)\cos{\theta} \cdot d\vec{v}_i \tag{3.4} \]
我们上文刚刚讨论过,最终brdf的定义为公式\((1.5)\),那么对于入射方向为\(\vec{l}\),出射方向为\(\vec{v}_i\)上的brdf,有
\[ f(\vec{l}, \vec{v}_i) = \frac{dL(\vec{v}_i)}{dE_{in}(\vec{l})} \]
公式\((3.4)\)里的\(L(\vec{v}_i)\)便是这里的分子部分了,即入射辐射通量为从\(\vec{l}\)方向时的微分辐射照度时,在出射方向上的辐射亮度。所以公式\((3.4)\)可化为如下公式。
\[ P_{out} = \int_{\vec{v}_i \in \Omega} f(\vec{l}, \vec{v}_i)dE_{in}(\vec{l}) \cdot \cos{\theta} \cdot d\vec{v}_i \tag{3.5} \]
如果不考虑其他的能量损耗,遵循能量守恒的理想情况下,我们认为入射的辐射通量与出射的辐射通量是相等的,即\(P_{in} = P_{out}\),即联立公式\((3.1)(3.5)\)有
\[ dE_{in}(\vec{l}) = \int_{\vec{v}_i \in \Omega} f(\vec{l}, \vec{v}_i)dE_{in}(\vec{l}) \cdot \cos{\theta} \cdot d\vec{v}_i \tag{3.6} \]
又因为\(dE_{in}\)与出射方向\(\vec{v}_i\)无关,所以对于右边的积分项来说,\(dE_{in}\)是常量,可以提到积分外面来。同时由前面已经描述过的lambert定律,brdf在任意出射方向都是相同的,也与出射方向无关,所以其对于右边的积分项来说,也是常量,也可以提到积分外面来,即
\[ \require{cancel} \\ \cancel{dE_{in}(\vec{l})} = f(\vec{l}, \vec{v}_i)\cancel{dE_{in}(\vec{l})} \cdot \int_{\vec{v}_i \in \Omega} \cos{\theta} \cdot d\vec{v}_i \tag{3.7} \]
即最终的brdf项可以表示为
\[ f(\vec{l}, \vec{v}_i) = \frac{1} {\int_{\vec{v}_i \in \Omega} \cos{\theta} \cdot d\vec{v}_i} \tag{3.8} \]
从这个公式也可以看出来,lambert光照的brdf与入射方向\(\vec{l}\)也是没有任何关系的,所以它是一个常量,即对任意入射和出射方向,它的值是一个定值。
右侧分母是一个半球领域上的定积分,我们如果可以求出这个积分,就得出了该问题最终的答案。
求半球领域的定积分
我们目前只需关注上述公式的分母部分这个定积分,将其记为F,即
\[ F = {\int_{\vec{v}_i \in \Omega} \cos{\theta} \cdot d\vec{v}_i} \tag{3.9} \]
求半球积分常用的方法,就是将方程转化为极角坐标系下的形式,将微元立体角转化为在极角坐标系下俯仰角和偏航角的步进极小值的积,即将单位半球的表面像地球仪那样被无数多个经线和纬线划分成无数份,如图所示。
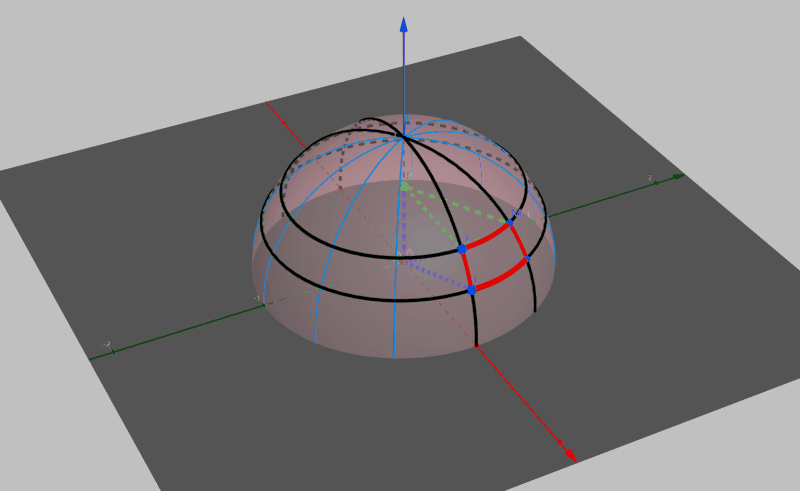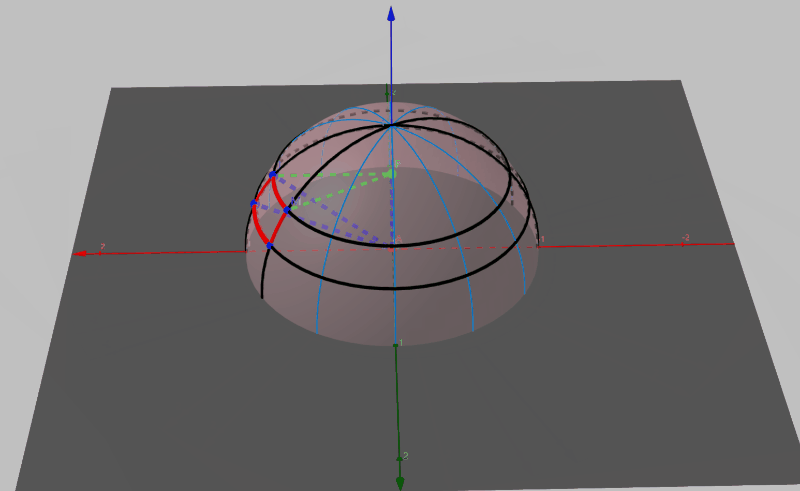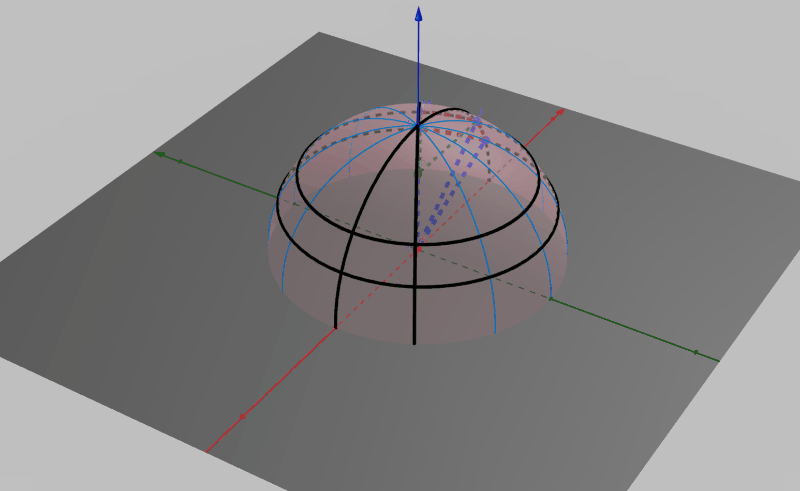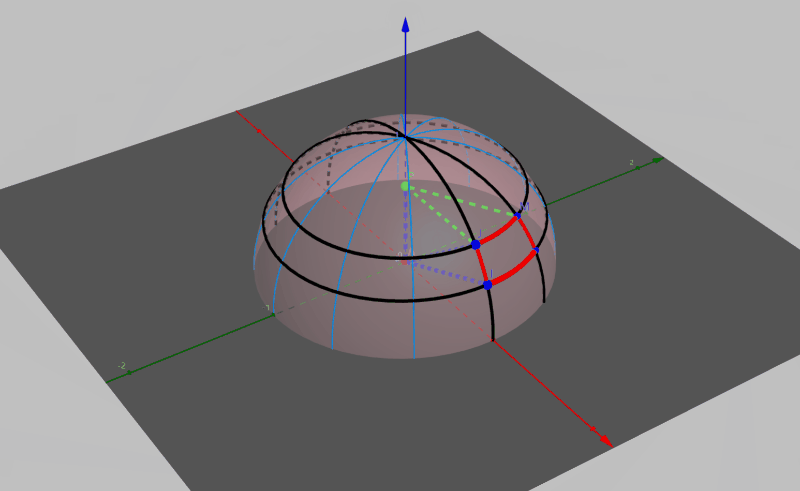
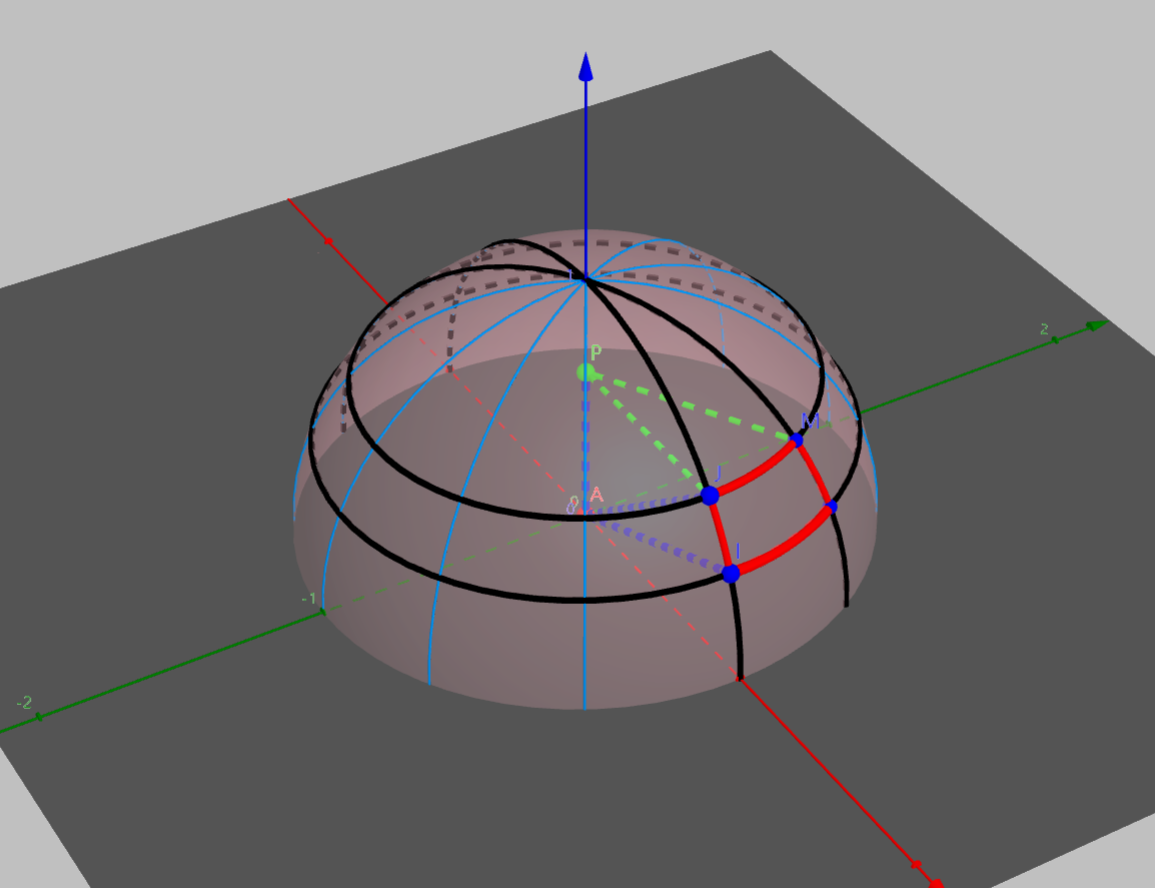
图中点P为点J在z轴上的投影,显然线段AP与线段AJ的夹角即为\(\theta\)。我们假设\(\theta\)在在俯仰角方向(即经线方向)的步进值为\(d\theta\),即为图中线段AJ与线段AI的夹角。假设在偏航方向(即纬线方向)的步进值为\(d\phi\),即为图中线段PJ与线段PM的夹角。那么由图中红色圆弧组成的曲面面积即为\(\theta\)方向上的微分立体角。
我们知道,弧长=半径*角度,所以\(d\theta\)所对应的弧长为
\[ \mathop{JI}\limits^{\frown} = r \cdot d\theta \]
而\(d\phi\)对应的圆弧所在的圆是以点P为圆心的一条纬线,这条圆的半径从上图中易得为
\[ r' = PJ = AJ \cdot \sin{\theta} = r \cdot \sin{\theta} \]
所在\(d\phi\)对应的圆弧弧长为
\[ \mathop{JM}\limits^{\frown} = r' \cdot d\phi = r\sin{\theta} \cdot d\phi \]
所以\(\theta\)方向上的微分立体角如下,其中由于是单位球体,所以半径r值为1可约去。
\[ \require{cancel} \\ d\vec{v}_i = \mathop{JI}\limits^{\frown} \cdot \mathop{JM}\limits^{\frown} = \cancel{r^2 \cdot} \sin{\theta}d\phi \cdot d\theta \tag{3.10} \]
由此,可将积分方程\((3.9)\)转化为在极角坐标系下的关于俯仰角和偏航角的二重积分,即
\[ F = \int_{\theta=0}^{\theta < \pi} \int_{\phi=0}^{\phi < 2\pi} \cos\theta \cdot \sin\theta \cdot d\theta d\phi \tag{3.11} \]
这个二重积分就可以很常规地解出来了,求解过程如下所示。
\[ \begin{array}{l} F = \int\limits_{\theta=0}^{\theta < \pi} \int\limits_{\phi=0}^{\phi < 2\pi} \cos\theta \cdot \sin\theta \cdot d\theta d\phi \\ = \int\limits_{\phi=0}^{\phi < 2\pi} [\frac{1}{2}\int\limits_{\theta=0}^{\theta < \pi} \sin{2\theta} d\theta] \cdot d\phi \\ = \frac{1}{2} \int\limits_{\phi=0}^{\phi < 2\pi} [-\frac{1}{2}\cos{2\theta}]_{0}^{\pi} \cdot d\phi \\ = \frac{1}{2} \int\limits_{\phi=0}^{\phi < 2\pi} [(-\frac{1}{2}\cos{\pi})-(-\frac{1}{2}\cos{0})] \cdot d\phi \\ = \frac{1}{2} \int\limits_{\phi=0}^{\phi < 2\pi} 1 \cdot d\phi \\ = \frac{1}{2} [\phi]_0^{2\pi} \\ = \frac{1}{2} [2\pi - 0] \\ = \pi \end{array} \tag{3.12} \]
其所用到的三角函数公式如下。
\[ \sin{2x} = 2 \cdot \sin{x} \cdot \cos{x} \\ \int \sin{cx} \cdot dx = -\frac{1}{c} \cos{cx} \]
将上式结果代入\((3.8)\),得
\[ f(\vec{l}, \vec{v}_i) = \frac{1}{\pi} \tag{3.13} \]
得证。\(^o^)/
后记
其实本文主要想说的是,在分析光照相关积分方程的时候,个人感觉比较重要的一点是要认清划分半球领域的单位是什么,可能是将半球领域划分成无穷多个立体角,每一个都是一个无穷小的微元,也可能是将半球领域划分成有限个立体角,比如\(2\pi\)个单位立体角,此时的微分方程可能就变成了这\(2\pi\)个方向上的值累加的结果。
不管划分成什么,只要根据能量守恒来联立方程,那么我相信最终得到的结果大概率是逻辑融洽,殊途同归的。
有时候划分成微元求积分的情况下不好理解和分析,那么就可以尝试一下通过划分成有限的份数来简化问题(难不成这就是传说中的有限元理论?),或者二者对比进一步验证问题,可能会更加准确地理解前辈先贤们到底栽的是什么树,种的是什么花,也就可以以更舒服的姿势乘凉了。
第二个后记
行文至此,一时收不住笔,最后顺便写一下这两年的感悟,聊以自省。
出来工作将近两年了,感觉自己相对来说算是幸运的吧,并没有感受到传说中的那种社会险恶,反而是遇见的人都对我很好,感受到了很多帮助和包容,也认识了一些有趣的人。
工作上就没有什么起色了。工作两年下来,感觉专业能力上并没有什么特别大提升,可能一些软技能,比如跟策划、后台同学对需求、改bug的能力倒是提升了不少-_-。
每天面对着无穷无尽并且时时变化着的需求和bug,确实容易消沉,自我印象我并非一个容易消沉的人,但却也确实消沉了很长一段时间,工具人做久了,可能就会像心灵鸡汤里说的那样慢慢与自己"和解"了吧,但是这一份"和解"中,或多或少会夹杂着一些意难平吧。
每一个人的精神追求都是不同的,如果一个人在尝试解读别人的行为的时候,会先去尝试理解和尊重这个人的精神追求,也许这个世界上孤独的人就会少很多吧。毕竟很多人可能并不在意精神追求这回事,不知是幸运还是不幸,我大概是不属于这一类人吧。
有些遗憾的是,我开始逐渐接纳如今慵懒堕落的自己,伴随着信心,热情也在褪色。所幸我时不时都想用微不足道的力量去反抗一下,即便这力量越来越弱,也可以拿来欺骗自己一段时间。
所以才有了这一篇博客,虽然粗浅,但大概是我这两年来与内心博斗的所有战果了。悲凉寒碜,没有关系。没有价值,我不在乎。是因为当完成之时,心里的确有一丝暖流流过。虽只一丝,但可能也就指这个活着呢。
可以与自己和解,但是也要学会奉劝自己,最好不要轻易丢弃对于真正热爱的东西最原始而纯粹的那份追求。
共勉。