【cg】常见的空间加速结构

发表于 更新于 分类于 阅读次数： 本文字数： 11k 阅读时长 ≈ 10 分钟

前言

本文开始介绍一些常见的空间加速结构，这些加速结构可能会被广泛地应用于各个开发场景，在渲染、光线追踪等情境下尤甚。本文是一个开始，只入门性质地介绍一些浅显的理论和精简的实现。

常见的空间加速结构

八叉树(Octree)是一种耳熟能详的数据结构，它本质上二叉树(Binarytree)及四叉树(Quadtree)没什么区别。只不过在树的规模，划分的维度上有些区别，但划分的方法都是绝对公平的均匀划分。

四叉树会均匀地将平面划分为四等份，然后继续递归划分。

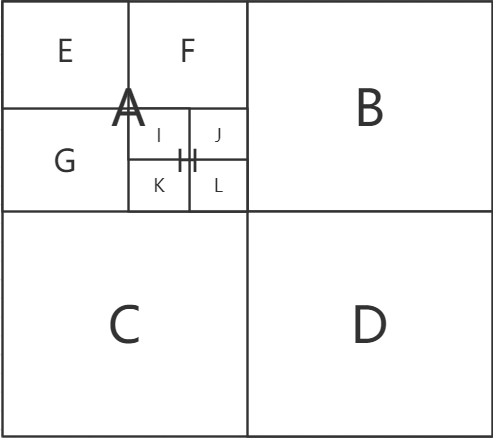
Quadtree

八叉树会均匀地将空间划分为八等份，然后继续递归划分。所以八叉树的节点是基于空间的，代表着场景空间中的一块区域。

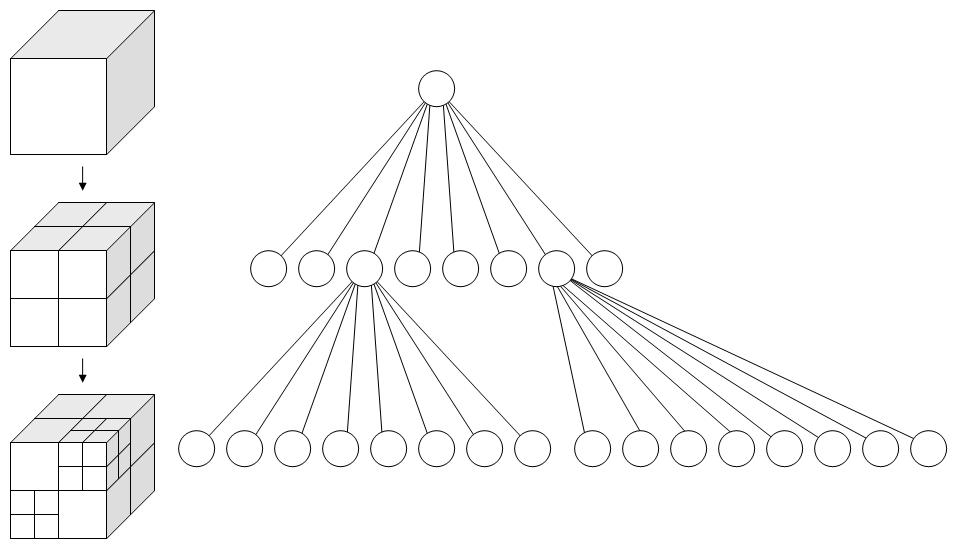
Octree

八叉树的实现相当简单，会写二叉树的同学十六叉树应该也是信手拈来。关于其在工程上的实现后文会提到。而其在算法上的实现，这里可以参考一道古老的关于四叉树的算法题稍作了解。

Quadtrees UVA-297

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
char s1[maxn], s2[maxn];
int id, deep;

const int root = 1;
int Left[maxn], Right[maxn], Up[maxn], Down[maxn], cnt;
int val[maxn];

void init() {
    Left[root] = Right[root] = Up[root] = Down[root] = 0;
    cnt = root;
    met(val, 0);
}

int newnode() {
    int u = ++cnt;
    Left[u] = Right[u] = Up[u] = Down[u] = 0;
    return u;
}

void build(char s[], int rt, int depth) {
    if(s[id] == 'f') {
        if(val[rt] == 0) val[rt] = 1;
        Left[rt] = Right[rt] = Up[rt] = Down[rt] = 0;

    }
    else if(s[id] == 'e') {}
    else {
        if(Left[rt] == 0) Left[rt] = newnode();
        ++id; build(s, Left[rt], depth+1);
        if(Right[rt] == 0) Right[rt] = newnode();
        ++id; build(s, Right[rt], depth+1);
        if(Up[rt] == 0) Up[rt] = newnode();
        ++id; build(s, Up[rt], depth+1);
        if(Down[rt] == 0) Down[rt] = newnode();
        ++id; build(s, Down[rt], depth+1);
    }

}

int solve() {
    int ans = 0;
    queue<int> q, d;
    q.push(root); d.push(0);

    while(!q.empty()) {
        int t = q.front(); q.pop();
        int dp = d.front(); d.pop();
        if(val[t] == 1) { ans += pow(4,deep-dp); continue; }
        if(Left[t] != 0) q.push(Left[t]), d.push(dp+1);
        if(Right[t] != 0) q.push(Right[t]), d.push(dp+1);
        if(Up[t] != 0) q.push(Up[t]), d.push(dp+1);
        if(Down[t] != 0) q.push(Down[t]), d.push(dp+1);
    }
    return ans;
}

从实现上看一般分为两个步骤，建树和查询。其中建树过程会递归地划分场景空间直到达到最小粒度。而查询则是普通树的深搜或者广搜。

对于动态变化的场景，我们可能还会额外添加物体进入和离开某个八叉树节点的条件，比如离开时需要远离到更大的距离才算离开，防止某物体在两个节点间反复横跳。这种八叉树又被叫做是松散的。

八叉树可以应用于场景管理，特别是地广人稀的室外空间的管理。还会被用在光线追踪、物理碰撞检测等方面。

bvh树又称层次包围盒(bounding volume hierarchy based on tree)。

bvh树是一个二叉树，每个节点最多只有两个子节点。

bvh树的节点与八叉树不同，它并不是基于空间的，而是基于场景中物体的图元的，更准确的说，是基于图元的包围盒的。它首先需要将场景中所有的物体的图元(物体本身、物体的一部分或三角形面片等各个粒度都可)的包围盒(AABB包围盒或球形包围盒都可)作为输入。

bvh

bvh树的建树过程也是一个递归的过程。它需要将场景中所有的图元加到根结点上，然后从根节点递归地进行划分，直到某节点的图元数量为1或者达到最小粒度终止。

其一次划分的结果是给当前被划分的节点生成了左右两个子节点，子节点的内容是其包含的图元列表。然后再分别用同样的方式划分左右两个子节点。划分一个节点的过程大致如下。

1.首先遍历当前节点的所有图元，构建一个最小的包含所有图元的中心点的包围盒，并求出这个包围盒最长的那个轴。

2.延该轴进行划分，划分的方法有很多种，这里介绍一下其中比较经典的一种SAH(surface area heuristic)。

SAH

如上图所示。这种方法首先把场景按该轴的方向划分成多个同等宽度的桶bucket。

然后遍历当前节点的所有图元，将它们放到它们的中心点所性的bucket里，并更新bucket的包围盒大小。至此生成完备的bucket数据。

然后遍历每一个bucket，求如果以这个bucket作为分界线划分右左右两个子节点会产生多少消耗。从中选取消耗最小的bucket作为划分的边界。将该bucket左边的所有bucket里的图元放到左子节点里，右边的放到右子节点里。

而消耗的计算，则使用以下公式。

\[ c(A, B) = t_{trav} + P_A \sum^{N_A}_{i=1} t_{isect}(a_i) + P_B \sum^{N_B}_{i=1} t_{isect}(b_i) \tag{3.1} \]

其中\(t_{trav}\)和\(t_{isect}\)是两个可配置的与光线追踪有关的系数，这里可以认为是常数。\(P_A、P_B\)分别是两边包围盒的大小占该节点总包围盒大小的面积比例。\(N_A、N_B\)分别是两边所拥有的图元数量。

上述公式转换成求每个bucket的消耗的代码如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
<<Compute costs for splitting after each bucket>>=
Float cost[nBuckets - 1];
for (int i = 0; i < nBuckets - 1; ++i) {
    Bounds3f b0, b1;
    int count0 = 0, count1 = 0;
    for (int j = 0; j <= i; ++j) {
        b0 = Union(b0, buckets[j].bounds);
        count0 += buckets[j].count;
    }
    for (int j = i+1; j < nBuckets; ++j) {
        b1 = Union(b1, buckets[j].bounds);
        count1 += buckets[j].count;
    }
    cost[i] = .125f + (count0 * b0.SurfaceArea() +
                       count1 * b1.SurfaceArea()) / bounds.SurfaceArea();
}

3.对划分出来的左右子节点同样进行步骤1、2，直到图元数量为1或者达到最小粒度终止。

以上过程可参考pbrt 4.3 Bounding Volume Hierarchies

在pbrt里介绍了很多种划分方法，上面只是其中一种SAL。

1
2
<<BVHAccel Public Types>>=
enum class SplitMethod { SAH, HLBVH, Middle, EqualCounts };

可以看出，正因为bvh树的节点是基于图元而非基于空间的，所以它具有更灵活的粒度来分割物体，比八叉树更适合用于光线追踪，划分效率更高。

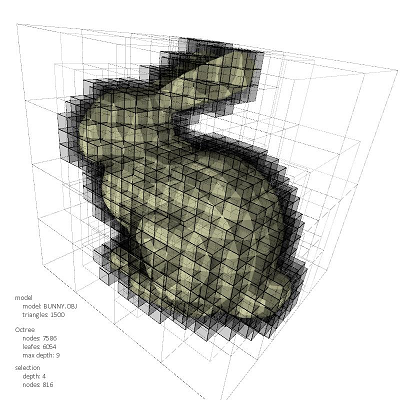
rabit by octree
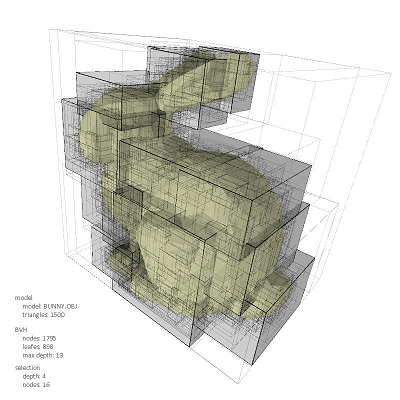
rabit by bvh

我们也可以选择不同类型的包围盒参与bvh树的划分，如AABB包围盒可以生成AABB层次包围盒树，或者最简单的球体包围盒生成球体树，都有其异同和优缺点。

k-d树(k-dimensional tree)也是一个二叉树，每个节点也是最多只有左右两个子节点。

k-d树的节点也不是基于空间的，也是和物体相关的，但它并非是真正服务于物体的，而是真正服务于坐标点的。我们会将场景中所有物体的中心坐标点作为数据输入来建树。

k-d树的建树过程也是递归的。首先需要将所有的坐标点作为输入数据加到根节点上，其递归过程大致如下。

1.对于当前节点的所有坐标点，选择一个方差最大的维度作为其主维度开始进行划分。

2.在主维度上，选定中值所在的坐标点作为当前节点的主坐标点，经过该坐标点并与主维度垂直可确定一个唯一的平面，这个平面称作超平面，每个节点其实代表着一个超平面。

3.在主维度上小于中值的坐标点放在左节点上，大于的放在右节点上，生成当前节点两个子节点。

4.对各个子节点，重复步骤1、2、3直到不可继续划分或达到划分粒度。

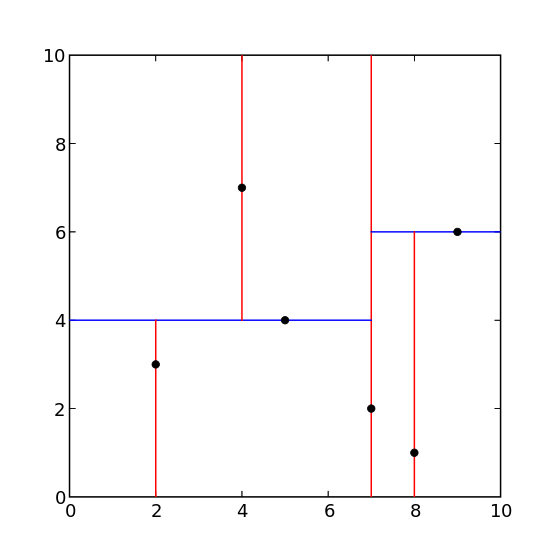
k-d tree build
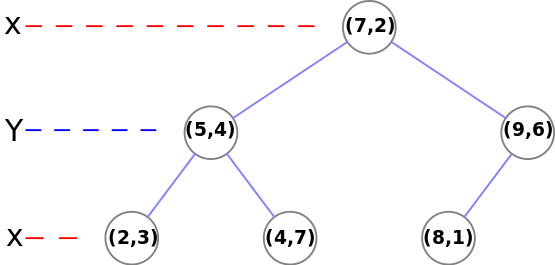
k-d tree result

k-d树其实在每个维度上都是一个相对严格的二叉树，只不过各个维度的数据交错起来了。在一个维度上生成二叉树的时间复杂度是O(nlogn)，所以k-d树的建树时间复杂度为\(O(k \cdot nlogn)\)。

k-d树的查询是极快的O(logn)，因为对于每一个节点来说，都只需要比较它的某一个维度的数据。所以它经常被用作给定坐标点的最近邻查询，即查询与给定坐标点最接近的k个点及其最近距离。即使是进行区间查询，k-d树的时间复杂度也可以达到\(O(k \cdot n^{1-\frac{1}{k}})\)。

其在算法上的实现也可以参考一道老题。

HDU-4347 The Closest M Points

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
struct Point
{
    int x[maxk];
    bool operator<(const Point &o)const
    {
        return x[idx]<o.x[idx];
    }
}poi[maxn];
typedef pair<double,Point> P;
priority_queue<P> Q;

struct kdTree
{
    #define sqr(x) ((x)*(x))
    #define ls (rt<<1)
    #define rs (rt<<1|1)

    int k;
    Point o[maxn<<2];
    int son[maxn<<2];

    void build(int rt, int l, int r, int dep)
    {
        if(l > r) { return; }
        son[rt] = r-l, son[ls] = son[rs] = -1;

        idx = dep % k;
        int mid = (l+r) >> 1;
        nth_element(poi+l, poi+mid, poi+r+1);
        o[rt]=poi[mid];

        build(ls,l,mid-1,dep+1);
        build(rs,mid+1,r,dep+1);
    }

    void query(int rt, Point p, int m, int dep)
    {
        if(son[rt] == -1) { return; };
        P nd(0, o[rt]);
        for(int i = 0; i < k; i++) { nd.fi += sqr(nd.se.x[i]-p.x[i]); }

        bool fg=0;
        int dim = dep % k, x = ls, y = rs;
        if(p.x[dim] >= o[rt].x[dim]) { swap(x, y); }

        if(~son[x]) { query(x, p, m, dep+1); }

        if(Q.size() < m)
        {
            Q.push(nd);
            if(~son[y]) { query(y, p, m, dep+1); }
        }
        else
        {
            if(nd.fi < Q.top().fi) { Q.pop(); Q.push(nd); }
            if(sqr(p.x[dim] - o[rt].x[dim]) < Q.top().fi)
            {
                if(~son[y]) { query(y, p, m, dep+1); }
            }
        }
    }
}kdtree;

像这种以超平面为节点的二叉空间分割树，有一个更一般的数据结构叫做bsp树(binary space partitioning tree)，其每个节点的超平面可以是任意超平面。

bsp truee

所以k-d树实际上是一种特殊的bsp树，它是超平面只与坐标轴平行的bsp树。

由于可以是任意超平面，所以bsp树的构建比k-d树要更复杂些，主要原因是判断该超平面与物体的关系时的情况有些复杂，无法像k-d树那样只通过一个维度的数据就可判断，而且还有可能出现同一个物体有一部分在超平面前，有一部分在超平面后的情况，此时则需要进一步分割物体，使其一部分添加在前方的节点里，一部分添加在后方的结点里。

可以发现，上述三者一个最明显的区别就是节点内容。

八叉树的节点内容是空间的区域以及该区域内的物体列表。

bvh树的节点内容是场景中的划分到该节点的图元(及其包围盒)列表。

k-d树的节点内容是三维的空间坐标点，以及当前深度的维度，从而确定一个当前节点所代表的超平面。

上面是各加速结构在算法上的原理及实现，但在工程上的实现却又不完全是那么回事，下面以unreal中的八叉树实现来体会一下。

unreal中的八叉树实现

八叉树(Octree)在ue4中工程化的实现方式的大部分代码位于Engine\Source\Runtime\Engine\Public下的GenericOctree.h和GenericOctree.inl。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

/** An octree. */
template<typename ElementType,typename OctreeSemantics>
class TOctree
{
public:

    typedef TArray<ElementType, typename OctreeSemantics::ElementAllocator> ElementArrayType;
    typedef typename ElementArrayType::TConstIterator ElementConstIt;

    /** A node in the octree. ============================== */
    class FNode
    {
    public:
        friend class TOctree;
        explicit FNode(const FNode* InParent);
        ~FNode();
    private:
        mutable ElementArrayType Elements;
        const FNode* Parent;
        mutable FNode* Children[8];
        mutable uint32 InclusiveNumElements : 31;
        mutable uint32 bIsLeaf : 1;
    };
    /** A node in the octree. ============================== */

    /** An octree node iterator. =========================== */
    template<typename StackAllocator = DefaultStackAllocator>
    class TConstIterator
    {
    public:
        void PushChild(FOctreeChildNodeRef ChildRef);
        void Advance();
        bool HasPendingNodes() const;
        FNodeReference CurrentNode;
        TArray<FNodeReference,StackAllocator> NodeStack;
    };
    /** An octree node iterator. =========================== */

    void AddElement(typename TTypeTraits<ElementType>::ConstInitType Element);
    void RemoveElement(FOctreeElementId ElementId);

    TOctree(const FVector& InOrigin,float InExtent);

private:

    FNode RootNode;
    FOctreeNodeContext RootNodeContext;
    float MinLeafExtent;

    void AddElementToNode(
        typename TTypeTraits<ElementType>::ConstInitType Element,
        const FNode& InNode,
        const FOctreeNodeContext& InContext
    );
};

这是一个模板类。其模板参数ElementType是每个节点的真正内容。OctreeSemantics是模板的辅助语义，它使得使用者在该类中某些固定的流程结构中定制特定的步骤或数据，这在设计模式中称为模板方法模式(Template Method)。

以ue4场景中的物体为例，它使用了以下类型作为模板参数来达到定制化的八叉树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
typedef TOctree<class FPrimitiveSceneInfoCompact,struct FPrimitiveOctreeSemantics> FScenePrimitiveOctree;

class FPrimitiveSceneInfoCompact
{
    // ...
};

struct FPrimitiveOctreeSemantics
{
    enum { MaxElementsPerLeaf = 256 };
    enum { MinInclusiveElementsPerNode = 7 };
    enum { MaxNodeDepth = 12 };

    typedef TInlineAllocator<MaxElementsPerLeaf> ElementAllocator;

    FORCEINLINE static const FBoxSphereBounds& GetBoundingBox(const FPrimitiveSceneInfoCompact& PrimitiveSceneInfoCompact)
    {
        return PrimitiveSceneInfoCompact.Bounds;
    }

    FORCEINLINE static bool AreElementsEqual(const FPrimitiveSceneInfoCompact& A,const FPrimitiveSceneInfoCompact& B)
    {
        return A.PrimitiveSceneInfo == B.PrimitiveSceneInfo;
    }

    FORCEINLINE static void SetElementId(const FPrimitiveSceneInfoCompact& Element,FOctreeElementId Id)
    {
        Element.PrimitiveSceneInfo->OctreeId = Id;
    }
};

建树参数

1
2
3
4
5
6
7
8
template<typename ElementType,typename OctreeSemantics>
TOctree<ElementType,OctreeSemantics>::TOctree(const FVector& InOrigin,float InExtent)
:   RootNode(NULL)
,   RootNodeContext(FBoxCenterAndExtent(InOrigin,FVector(InExtent,InExtent,InExtent)),0,0)
,   MinLeafExtent(InExtent * FMath::Pow((1.0f + 1.0f / (float)FOctreeNodeContext::LoosenessDenominator) / 2.0f,OctreeSemantics::MaxNodeDepth))
,   TotalSizeBytes(0)
{
}

构建一个八叉树需要以下参数。

Origin -- 树的原点。

Extent -- 树的范围(最大的包围盒)。

LoosenessDenominator -- 松散度分母，用于计算同级节点重合部分。由此也可以看出unreal实现的八叉树其实是一个松散八叉树。

MaxNodeDepth -- 最大的节点深度。

建树流程

unreal中的建树流程，即添加一个物体到八叉树中的流程，如下所示。

1.以根节点作为当前Node，开始使用迭代器遍历node。

这里的迭代器实现了一种深度优先遍历，它维护了一个以节点索引为元素的栈。

对于当前的节点，调用TConstIterator::PushChild()将其子元素压入栈顶。并调用TConstIterator::Advance()进行迭代，每次迭代将栈顶元素出栈。

2.如果当前节点非最终的叶子节点或者当前节点拥有的元素过多，则尝试创建其子节点。

创建子结点的规则是，如果某个子节点完全包含物体，则将该子节点压入迭代器，等下次迭代便可处理该子节点。

如果当前节点并没有子节点可以完全包含物体，则直接将该物体放入当前节点中。

3.如果当前节点为最小粒度的叶节点，则直接将物体放入其中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
template<typename ElementType,typename OctreeSemantics>
void TOctree<ElementType,OctreeSemantics>::AddElementToNode(
    typename TTypeTraits<ElementType>::ConstInitType Element,
    const FNode& InNode,
    const FOctreeNodeContext& InContext
    )
{
    const FBoxCenterAndExtent ElementBounds(OctreeSemantics::GetBoundingBox(Element));

    for(TConstIterator<TInlineAllocator<1> > NodeIt(InNode,InContext); NodeIt.HasPendingNodes(); NodeIt.Advance())
    {
        const FNode& Node = NodeIt.GetCurrentNode();
        const FOctreeNodeContext& Context = NodeIt.GetCurrentContext();
        const bool bIsLeaf = Node.IsLeaf();

        bool bAddElementToThisNode = false;

        Node.InclusiveNumElements++;

        if(bIsLeaf)
        {
            if(Node.Elements.Num() + 1 > OctreeSemantics::MaxElementsPerLeaf && Context.Bounds.Extent.X > MinLeafExtent)
            {
                Node.InclusiveNumElements = 0;
                Node.bIsLeaf = false;
                AddElementToNode(Element,Node,Context);
                return;
            }
            else { bAddElementToThisNode = true; }
        }
        else
        {
            const FOctreeChildNodeRef ChildRef = Context.GetContainingChild(ElementBounds);
            if(ChildRef.IsNULL()) { bAddElementToThisNode = true; }
            else
            {
                if(!Node.Children[ChildRef.Index])
                {
                    Node.Children[ChildRef.Index] = new typename TOctree<ElementType,OctreeSemantics>::FNode(&Node);
                }

                // iterate child node
                NodeIt.PushChild(ChildRef);
            }
        }

        // add to this node and return
        if(bAddElementToThisNode)
        {
            new(Node.Elements) ElementType(Element);
            OctreeSemantics::SetElementId(Element,FOctreeElementId(&Node,Node.Elements.Num() - 1));
            return;
        }
    }
}

后记

本文所阐述的空间加速结构只是一个初步的概念认识和简单实现，后续会继续更新一些使用细节和扩展，以及更高科技一些的使用方式，如在GPU上并行建树等具有实际价值的方法。但无论如何，掌握理论总是首要的。

我的博客即将同步至腾讯云开发者社区，邀请大家一同入驻：https://cloud.tencent.com/developer/support-plan?invite_code=3i6tlz41tbi8s