【cg】【原理】法线贴图

发表于 2020-02-24 更新于 2022-08-01 分类于 game_graphics 阅读次数：本文字数： 3.1k 阅读时长 ≈ 3 分钟

前言

在OpenGL中，每一个三角形面片，都是一个平坦的平面。在该平面上的所有像素点，其法线方向都是相同的。

我们知道，无论是传统的光照模型，还是基于物理的光照模型，法线决定平面的朝向，对于光照的计算至关重要。

所以一个模型的表面法线越接近于真实世界中的法线，获得的光照就越正确，光照细节就越多。

但是目前为止，我们的法线都是跟随顶点数据传到GPU的，并没有精确到像素级的(虽然传到片段着色器时会进行插值，但是同一个表面的法线始终是一样的)，这就导致在计算光照的时候我们只能得到平坦的平面，而丢失了平面的凹凸细节。比如，一个砖墙，由许多砖块组成，但是整个砖墙都只有一个法线朝向，完全忽略了砖与砖接缝处的凹凸痕迹。

于是法线贴图就应运而生了。

法线贴图

我们迫切地需要关于该平面上所有位置的法线信息，换句话说，我们希望所有的像素都能有自己的法线信息。那么自然而然地，使用一张与漫反射贴图同样大小的贴图，只不过每个像素点保存的信息是该像素点的法线信息而已。

这是可行的，因为颜色的rgb分量正好可以保存一个三维向量。

一般的法线贴图都是偏蓝色的，其原因也很容易理解，因为大部分的法线方向还是跟当前平面的整体朝向一致的，只有少数凹凸不平的地方才有不同的颜色。

我们也可以从中发现一个问题，一个平面在场景中可能通过了位移旋转等变换，那么同一个平面在不同情况下的法线肯定是完全不同的。所以法线贴图存储的法线方向，肯定是某一特殊情况的法线方向，而其他情况的法线方向都可以从此种情况变换过去。

这种特殊情况下的法线方向，应该是以平面的法线指向正z轴时的空间为基准的，这个空间就叫做切线空间。

切线空间的意思是，它是位于某面片上的空间，相当于法线贴图的本地空间。在这个空间里，面片的法线指向正z轴方向。而该空间的正y轴和正x轴方向，则与此表面的uv贴图对齐，此处的正x轴也称切线T(Tagent)，正y轴也称副切线B(Bitangent)。

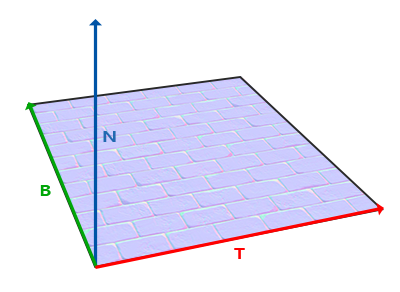
推导

通过计算切线空间的变换矩阵，即TBN矩阵，我们可以轻松实现切线空间与世界空间的坐标变换。

\[ \vec{V_{world}} = M_{tbn} \ast \vec{V_{tangent}} \tag{1.1} \]

\[ \vec{V_{tangent}} = M_{tbn}^{-1} \ast \vec{V_{world}} \tag{1.2} \]

所以我们接下来的任务就计算TBN矩阵，很明显TBN矩阵就是一个切线空间的向量基矩阵。即

\[ M_{tbn} = \begin{bmatrix} \vec{T} \\ \vec{B} \\ \vec{N} \\ \end{bmatrix} \tag{1.3} \]

那么，我们的任务就变成了计算这三个互相垂直的向量了。

法线向量很容易求得，只要用三角形面片的三个顶点组成的两个向量作叉积即可，这里不再赘述。

那么剩下的就是切线和副切线。它们有一个特点，就是与纹理坐标的两个方向对齐，所以我们可以通过纹理坐标来进行计算。如下图。

设\(P_1\)、\(P_2\)、\(P_3\)为三角形面片的三个顶点。

设\(\vec{E_1} = \vec{P_2P_1}\)，设\(\vec{E_2} = \vec{P_2P_3}\)。

设 \(\Delta U_1 = P_1.x - P_2.x\)；设 \(\Delta V_1 = P_1.y - P_2.y\)。

设 \(\Delta U_2 = P_3.x - P_2.x\)；设 \(\Delta V_2 = P_3.y - P_2.y\)。

则有

\[ \begin{cases} \vec{E_1} = \Delta U_1 \ast \vec{T} + \Delta V_1 \ast \vec{B}, \\ \vec{E_2} = \Delta U_2 \ast \vec{T} + \Delta V_2 \ast \vec{B}, \\ \end{cases} \tag{1.4} \]

即

\[ \begin{bmatrix} \vec{E_1} \\ \vec{E_2} \\ \end{bmatrix} = \begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \\ \end{bmatrix} \begin{bmatrix} \vec{T} \\ \vec{B} \\ \end{bmatrix} \tag{1.5} \]

那么

\[ \begin{bmatrix} \vec{T} \\ \vec{B} \\ \end{bmatrix} = \begin{bmatrix} \Delta U_1 & \Delta V_1 \\ \Delta U_2 & \Delta V_2 \\ \end{bmatrix}^{-1} \begin{bmatrix} \vec{E_1} \\ \vec{E_2} \\ \end{bmatrix} \tag{1.6} \]

二阶矩阵求逆，得

\[ \begin{bmatrix} \vec{T} \\ \vec{B} \\ \end{bmatrix} = \frac{1}{\Delta U_1 \Delta V_2 - \Delta U_2 \Delta V_1} \begin{bmatrix} +\Delta V_2 & -\Delta V_1 \\ -\Delta U_2 & +\Delta U_1 \\ \end{bmatrix} \begin{bmatrix} \vec{E_1} \\ \vec{E_2} \\ \end{bmatrix} \tag{1.7} \]

求得，转化为代码如下。

/* 根据三个顶点获得tbn矩阵 */
mat3 get_tbn(Vertex a, Vertex b, Vertex c) {

    vec3 e1 = b.position - a.position;
    vec3 e2 = c.position - a.position;

    vec2 d1 = b.tex_coord - a.tex_coord;
    vec2 d2 = c.tex_coord - a.tex_coord;

    // 行列式
    float f = 1.0f / (d1.x * d2.y - d2.x * d1.y);

    vec3 t_tangent = f * ( d2.y * e1 - d1.y * e2);
    vec3 t_bitange = f * (-d2.x * e1 + d1.x * e2);

    // 法线 -- 直接对两向量作叉积即可
    vec3 t_normal = normalize(cross(e1, e2));

    return mat3(t_tangent, t_bitange, t_normal);
}

下面为笔者引擎中实现的法线贴图效果。

无法线贴图	有法线贴图

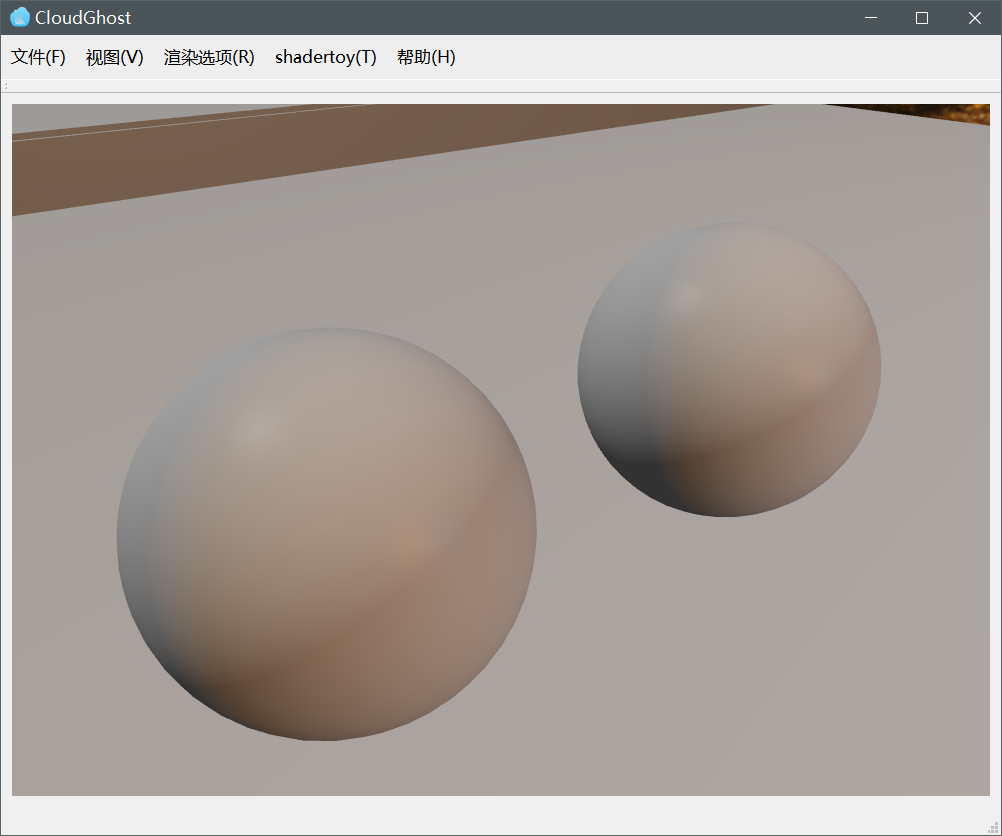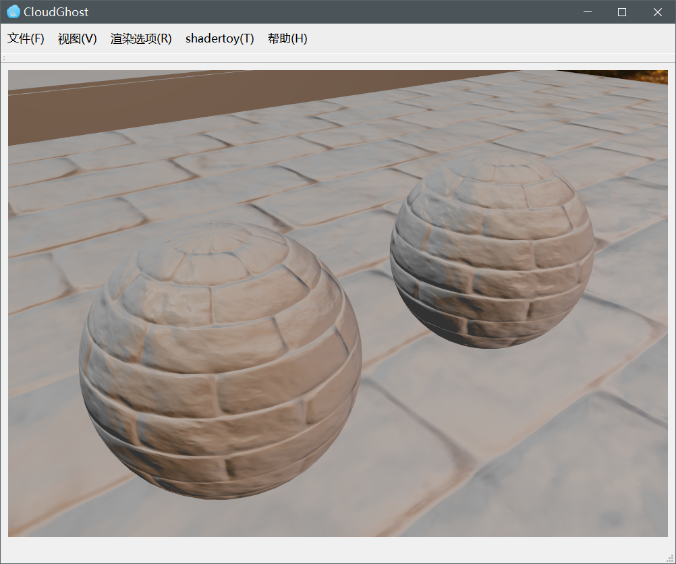结语

对于TBN矩阵中的三个正交向量基，显然我们可以知二求一。

比如说，我们目前只知道 N 和 T，如果要求 B 的话，只需要将N、T叉乘一下。但是在叉乘的过程中要注意方向。

很多时候，我们有一个法线向量，同时也有一个确定的上向量，但是这个上向量可能不是最终的正交向量基，它只是存在于由法线和切线(或副切线)向量组成的面上。但是通过法线与其叉乘，我们可以求出与这个面垂直的另一个向量，从而知二求一，再求出真正的切线(或副切线)向量。

所以我们在经常会用过类似于这样的代码。

/* 求切线空间向量基 -- 计算TBN矩阵 */
t_normal = normalize(p_normal);                 // N
// 上向量
t_up = vec3(0.0, 1.0, 0.0);
t_right = normalize(cross(t_up, t_normal));     // T
t_up = normalize(cross(t_normal, t_right));     // B

就是通这种不断地cross、normalize、cross，我们最终会得到三个互相垂直的单位向量，用来进行坐标空间的转换。

总而言之，这是一个不可多得的小连招~

\(^o^)/