【cg】【pbr】基于物理的渲染实现篇之间接光照(中)

发表于 更新于 分类于 阅读次数： 本文字数： 15k 阅读时长 ≈ 13 分钟

前言

书接上文，让我们继续来实现IBL，上回我们实现了低频域的漫反射间接光，即下面反射率方程的左边部分。

\[ L(p, \vec{v}) = \int_{\vec{l}_i \in \Omega} f_d \ast L(p, \vec{l}_i) \ast (\vec{n} \cdot \vec{l}_{i}) \ast d\vec{l}_i + \int_{\vec{l}_i \in \Omega} f_s \ast L(p, \vec{l}_i) \ast (\vec{n} \cdot \vec{l}_{i}) \ast d\vec{l}_i \tag{0.1} \]

那么本篇则是实现该方程的右边部分。

\[ L_{specular}(p, \vec{v}) = \int_{\vec{l}_i \in \Omega} f_s \ast L(p, \vec{l}_i) \ast (\vec{n} \cdot \vec{l}_{i}) \ast d\vec{l}_i \tag{0.2} \]

这也是一个连续型的积分，所以也需要通过离散化的方程去计算积分，但是这里不能再使用前文提到的黎曼和的方法，因为镜面反射项对精度要求更高，是一个高频域的信号。所以这里采用的是使用重要性采样加速的蒙特卡洛积分, 该方法又称Brute force specular IBL, 很暴力。

下面分别介绍蒙特卡洛积分和重要性采样的数学原理，以及我们为了实现specular IBL真正的采样手段所需要的前置数学知识。笔者主观意识里是比较想把这部分拆解清楚的，所以并不会吝啬篇幅(又不是写毕设)，所以内容可能有些小长，建议脾气暴躁者先码后看。

蒙特卡洛积分

蒙特卡洛积分(Monte Carlo integration)并不是某一个具体的积分方程，而是一种近似计算连续性积分的方法，这个方法是直接对整个积分区间进行一定数目的分布采样，计算这些采样点的具体值，并取所有采样点的具体值的平均值，以获得接近原积分的结果。

考察如下一般格式的连续性积分。

\[ F(x) = \int_{a}^{b} f(x) dx \tag{1.1} \]

我们在区间[a, b]上对其进行N次均匀采样，则有

\[ F(x) = \int_{a}^{b} f(x) dx \approx \frac{b - a}{N} \sum_{i = 0}^{i \lt N} f(x_i) \tag{1.2} \]

这便是使用蒙特卡洛方法近似求连续性积分的方法了。

重要性采样

重要性采样(importance sampling)是用来优化蒙特卡洛积分关于采样点的选取的。

在原始的蒙特卡洛积分中，其采样是均匀分布的，即每隔一个固定的时间(或空间)间隔采样一次。但是这样的坏处是，被积函数\(f(x)\)并非均匀分布的，这就导致并非所有的采样点的值对最终积分结果的贡献是一样的。而重要性采样便是确保采样点中对最终积分贡献大的点所占比例多。这样在相同的采样数目时，使用重要性采样计算的结果便更加准确。或者说在达到相同准确度的效果下，重要性采样需要的采样数目更少。

该方法使用被积函数\(f(x)\)本身的概论密度函数(probability density function, pdf)来构造采样点的分布情况。pdf是指随机变量(random variable, rv, 表示事件在某个区间发生的概率)在某个无穷小区间的概率值，即

\[ X[a, b] = \int_{a}^{b} p(x_i) dx_i \tag{1.3} \]

其中X[a, b]为随机变量X在区间[a, b]上发生的概率。而\(p(x_i)\)即为X在位置\(x_i\)上的概率值。即p(x)为X的概率密度函数pdf。

由此可见，随机变量是其概率密度函数的积分，概率密度函数是随机变量的微分。

对于被积函数\(f(x_i)\)来说，\(p(x_i)\)则为其在点\(x_i\)处的值占最终积分结果的比重，即对于公式\((1.1)\)，有

\[ F(x) = \frac{f(x_i)}{p(x_i)} \tag{1.4} \]

即我们可以仅通过一个采样点，根据pdf即可求出最终的积分结果，但是这个结果可能会存在较大的误差。如果我们跟蒙特卡洛积分一样，也选取N个采样点，即对N个点使用公式\((1.4)\)然后求其平均值，那么最终的蒙特卡洛积分将变为一个数学期望，如下公式所示。

\[ F(x) = \int_{a}^{b} f(x) dx \approx \frac{1}{N} \sum_{i = 0}^{i \lt N} \frac{f(x_i)}{p(x_i)} \tag{1.5} \]

这便是重要性采样了，我们选取pdf最高的N个点进行采样，当然比原来去均匀地选取N个点进行采样得到的结果要准确的多。

对于原始蒙特卡洛积分的均匀分布采样，其pdf为

\[ p(x) = \frac{1}{b - a} \tag{1.6} \]

将其代入\((1.5)\)即可得到原始的蒙特卡洛积分\((1.2)\)，这也验证了重要性采样的正确性。

采样分布映射

现在我们知道了要选择N个pdf最大的点进行采样，来近似求得最终的积分结果。但是却不知道要怎么样才能选择出这N个满足条件的点。

有一种方法是，一开始还是均匀地选择N个点，然后通过某种方法将其映射到某个函数上，得到新的N个点，而新得到的这些点里面，pdf值大的点所占的比重比较多，我们就认为这些点就是满足我们需要的点。这个过程便叫做采样分布映射。即从N个分布均匀的点，映射到N个满足我们需要的分布的点上。

反函数法

数学界有许多方法可以做到这一点，笔者这里要介绍的(也是笔者唯一知道的。。Orz)，叫做反函数法(inverse method)。

维基百科介绍

该方法将均匀分布的N个采样点，通过累积密度函数(cumulative density function, cdf)的反函数，来映射出新的N个采样点，映射出的新的点，便是我们需要的结果。

累积密度函数

累积密度函数(cumulative density function, cdf)是pdf从样本区间下限到当前采样点区间的概率值。

\[ cdf(x) = P(x) = \int_{a}^{x} p(x_i) dx_i \tag{1.7} \]

即cdf(x)为pdf在[a, x]上的积分，显然\(cdf \in [0, 1]\)。

开始映射

我们在cdf的y轴上均匀选取N个点\(y_1, y_2, ..., y_i, ..., y_n\)， 那么对任意\(i \in [1, n]\)，有

\[ y_i = cdf(x_i) \tag{1.8} \]

取反求\(x_i\)，得

\[ x_i = cdf^{-1}(y_i) \tag{1.9} \]

那么\(x_1, x_2, ..., x_i, ..., x_n\)则为我们最终的采样点位置。这便是inverse method。

举一个简单但可能并不形象的例子。

你买面值不超过1元的刮刮乐中奖的概率不超过0.1，买超过1元但不超过2元的中奖概率是不超过0.3，买超过2元但不超过3元的中奖概率不超过0.6。假设你最多只有3元钱(穷但不重要)。

那么现在我们的pdf是这样的:

p([0, 1]) = [0.0, 0.1] -- 记pdf_a

p((1, 2]) = (0.1, 0.3] -- 记pdf_b

p((2, 3]) = (0.3, 0.6] -- 记pdf_c

那么现在我们的cdf是这样的:

P([0, 1]) = [0.0, 0.1]

P((1, 2]) = (0.1, 0.4]

p((2, 3]) = (0.4, 1.0]

这个时候，我们均匀地选择cdf = 0.1, 0.2, ..., 0.9, 1.0处所对应的样本，就会发现超过2元的样本数目比较多。

超过2元的 -> 1.0, 0.9, 0.8, 0.7, 0.6, 0.5

超过1元不超过2元的 -> 0.4, 0.3, 0.2

不超过1元的 -> 0.1, 0.0

可以看到，对于我们最终产生的采样点，pdf越大的地方，采样点越密集，满足了重要性采样的要求。

也就是说，当我们从cdf的y轴上均匀地采样时，其映射在x轴上的点，在pdf大的地方密集，在pdf小的地方稀疏。

直观上也不难理解，因为pdf可以理解为cdf的导数，反应到函数图像上也就是cdf增长的速度，自然在增长速度快的地方，其取值区间越大，在均匀采样的情况下，落在区间内的点自然越多。

开始实现

有了上面的理论基础，下面就可以开启实现specular IBL的历程了。但是中间也会遇到各种需要补充的理论，由于笔者认为需要等实现到那一步时再去现场理解为什么需要这些理论来推动剧情发展，所以并没有把这些理论预先放在前面，而是放在了实现过程之中，以求可以更清楚地描述实现过程。

概率密度函数

首先，Cook-Torrance brdf specular的pdf函数如下。

\[ p_{s}(p, \vec{h_i}) = D(p, \vec{h_i}) \ast (\vec{n} \cdot \vec{h_i}) \tag{1.10} \]

其物理意义是法线分布函数D在法线\(\vec{n_i}\)方向上的投影，即在宏观平面上的投影。这是因为宏观平面的所有微平面，不管其微观法线朝向哪，其投影到宏观平面的总和，就组成了宏观平面本身(关于这个的详细描述可参考浅墨巨佬(%%%)的这篇法线分布函数相关总结来理解，我在这里只盗个图方便自己以后理解)。即

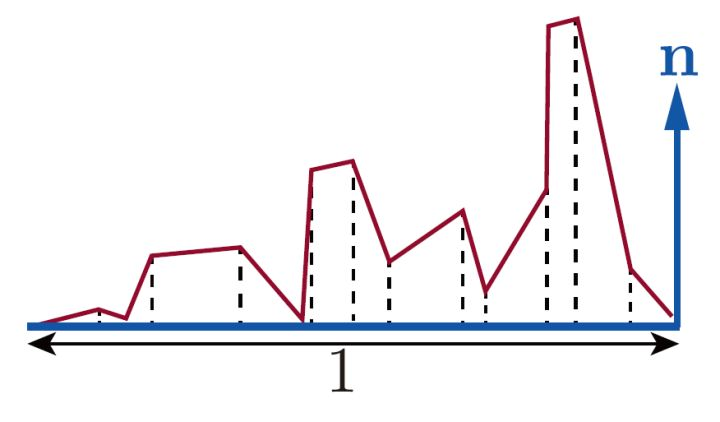
法线分布函数示意图

\[ \int_{\vec{h_i} \in \Omega} D(p, \vec{h_i}) \ast (\vec{n} \cdot \vec{h_i}) d\vec{h_i} = 1 \tag{1.11} \]

这也是概率密度函数所必须要满足的性质。

也许读者在其他地方，或者在本文后续的部分，发现pdf函数多了个分母，变成了下面这个样子，请不要惊讶。

\[ p_{s}(p, \vec{h_i}, \vec{v}) = \frac {D(p, \vec{h_i}) \ast (\vec{n} \cdot \vec{h_i})} {4 \ast (\vec{v} \cdot \vec{h_i})} \tag{1.12} \]

这是因为\((1.10)\)是以\(d\vec{h_i}\)为微元的，而在有些积分方程的计算里(后面就会碰到)，我们是以\(d\vec{l_i}\)为微元的，所以要乘以一下\(\frac{d\vec{h_i}}{d\vec{l_i}}\)才能将积分微元转换过来。这一点笔者也是过了好久(就在刚刚)才理解。

而在理论篇，我们已经证明过

\[ \frac{d\vec{h_i}}{d\vec{l_i}} = \frac{d\vec{h_i}}{d\vec{v}} = \frac{1}{ 4 \ast (\vec{l_i} \cdot \vec{h_i}) } = \frac{1}{ 4 \ast (\vec{v} \cdot \vec{h_i}) } \tag{1.13} \]

便是\((1.12)\)的形式了。

积分方程

由\((0.2)(1.5)\)可得

\[ L_{specular}(p, \vec{v}) \approx \frac{1}{N} \sum_{i = 0}^{i \lt N} \frac { f_s \ast L(p, \vec{l_i}) \ast (\vec{n} \cdot \vec{l_i}) } { p_{s}(p, \vec{l_i}, \vec{v}) } \tag{1.14} \]

代入\(f_s, p_s\)得

\[ \require{cancel} \\ L_{specular}(p, \vec{v}) \approx \frac{1}{N} \sum_{i = 0}^{i \lt N} \frac { F \ast G \ast \cancel{D(p, \vec{h_i})} } { 4(\vec{n} \cdot \vec{v}) \cancel{(\vec{n} \cdot \vec{l_i})} } \ast L(p, \vec{l_i}) \cancel{(\vec{n} \cdot \vec{l_i})} \ast \frac {4 (\vec{v} \cdot \vec{h_i})} {\cancel{D(p, \vec{h_i})} (\vec{n} \cdot \vec{h_i})} \tag{1.15} \]

即

\[ L_{specular}(p, \vec{v}) \approx \frac{1}{N} \sum_{i = 0}^{i \lt N} \frac { F(p, \vec{l_i}, \vec{v}) \ast G(p, \vec{l_i}, \vec{v}) \ast L(p, \vec{l_i}) \ast (\vec{v} \cdot \vec{h_i}) } { (\vec{n} \cdot \vec{v}) \ast (\vec{n} \cdot \vec{h_i}) } \tag{1.16} \]

这便是我们最终可以翻译成代码的公式了。可以看到，此时的微元是\(\vec{l_i}\)，所以我们使用\((1.12)\)形式的pdf函数进行代入。

现在唯一要解决的就只剩下这N个采样点的选择。

采样

正如上面采样分布映射所述，我们需要一开始确定N个均匀分布的点，然后再经过反函数法映射出N个点，这N个点满足在pdf大的地方密集的特点。

确定均匀分布的点

与上文所述不同的是， 我们最终需要在球面(半球领域)上采样，所以至上包含两个维度上的采样(经纬)，而且事实是我们也必须在两个维度上采样，所以我们确定均匀分布的点时，确认的便也是两个维度上的点，即我们要确定一个均匀的2D分布点集。

获取均匀的2D分布点集，也有很多办法，这里采取的是叫做哈默斯利采样(Hammersley sampling)的采样方法。

Hammersley sampling

该方法看起来高大上，其实仔细看一下原理却很简单，可以说是十分巧妙。

现在假设我们想采样N个点\(x_0, x_1, ..., x_i, ..., x_{N-1}\)，那么有

\[ x_i = (\frac{i}{N}, \Phi_2(i)) \]

其中\(\Phi_2(i)\)表示i的二进度位反转小数(radical inverse)，即将i的二进制位反转，然后再在最前面加上小数点即可。用公式来描述就是

\[ \Phi_2(i) = \frac{a_0}{2} + \frac{a_1}{2^2} + ... + \frac{a_r}{2^r} \]

其中\(i = a_0 + a_1 \ast 2 + a_2 \ast 2^2 + ... + a_r \ast 2^r\)，即\(a_0, a_1, ..., a_r\)分别是从右往左i的二进制位。

显然\(x_i.X \in [0.0, 1.0), x_i.Y \in [0.0, 1.0)\)。

可以参考下表理解。

i (十进制)i(二进制)\(\Phi_2(i)\) (二进制)\(\Phi_2(i)\) (十进制)
00000.00.00000.0
10001.00.10000.5
20010.00.01000.25
30011.00.11000.75
40100.00.00100.125
50101.00.10100.625
...
111011.00.11010.8125

当N = 16时，其在2D坐标系下的分布图像如下，

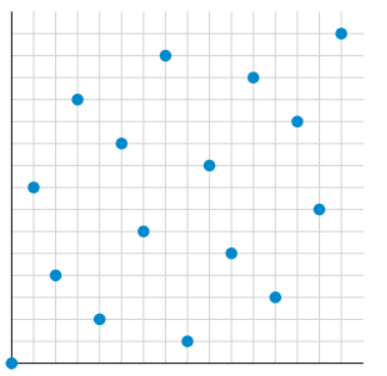
N=16时的Hammersley采样分布

至此，均匀分布的N个采样点便已经拿到了，其代码实现如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
float hammersley_radical_inverse(uint bits) {
    // inverse
    bits = ( bits << 16u ) | ( bits >> 16u );
    bits = ( ( bits & 0x55555555u ) << 1u ) | ( ( bits & 0xAAAAAAAAu ) >> 1u );
    bits = ( ( bits & 0x33333333u ) << 2u ) | ( ( bits & 0xCCCCCCCCu ) >> 2u );
    bits = ( ( bits & 0x0F0F0F0Fu ) << 4u ) | ( ( bits & 0xF0F0F0F0u ) >> 4u );
    bits = ( ( bits & 0x00FF00FFu ) << 8u ) | ( ( bits & 0xFF00FF00u ) >> 8u );
    // add 0.
    return float( bits ) * 2.3283064365386963e-10f;     // 2^(-32)
}

vec2 hammersley(uint i, uint sampler_num) {
    return vec2(
        float(i) / float(sampler_num),
        hammersley_radical_inverse(i)
    );
}

开始映射

有了上面均匀分布的N个采样点之后，我们开始使用前面介绍的反函数法，将其转变为N个满足重要性采样的点。

但是这里有一个问题是，前面介绍的反函数法似乎只是一个一维的算法，因为我们无法同时求两个维度的累积密度函数，所以需要将两个维度分开来处理，或者先求其中一个维度，然后在此基础上再求得另外一个维度的采样点。下面便是这个过程的具体细节。

对于pdf函数\((1.10)\)，由于在一次积分计算过程中，我们要计算的光照点\(p\)是不变的，所以我们不妨将pdf简记为如下方式，以方便后面的计算。

\[ p(\vec{h_i}) = D(p, \vec{h_i}) \ast (\vec{n} \cdot \vec{h_i}) \tag{1.17} \]

现在，为了分两个维度计算，我们将pdf函数改写成球面极角坐标系。观察pdf函数，可以看出，该函数对半程向量\(\vec{h_i}\)比较友好，反倒没有嗅到入射方向\(\vec{l_i}\)的踪影，所以这里我们将采样目标设定为半程向量，即我们最终拿到的N个采样点，是N个半程向量\(\vec{h_i}\)的方向。

设 \(\vec{h_i} = (\theta_i, \phi_i)\)，即\(\theta_i\)为该方向相对上轴(该点法线方向)偏移的角度。那么\(\vec{h_i}\)对应的立体角微分\(d\omega_i\)便为

\[ d\omega_i = d\theta_i \ast d\phi_i \ast \sin\theta_i \tag{1.18} \]

那么pdf函数的极角形式便如下公式所示。

\[ p(\theta_i, \phi_i) = p(\vec{h_i}) \ast \sin\theta_i = D(p, \vec{h_i}) \ast (\vec{n} \cdot \vec{h_i}) \ast \sin\theta_i = D(p, \vec{h_i}) \ast \cos\theta_i \ast \sin\theta_i \tag{1.19} \]

我们这里使用边缘分布(marginal distribution)来对其进行降维打击，将其打击成两个不相干的一维分布，就可使用上述的反函数法了，关于降维打击，，不，关于边缘分布的定义，请参考维基百科_边缘分布及其他资料，这里不作赘述。

我们先求关于\(\theta_i\)的边缘密度函数(marginal density function, mdf)。具体的求法便是，对于任意一个\(\theta_i\)，我们对所有的\(\phi_i\)进行积分，以消去\(\phi_i\)所产生的影响。

\[ mdf = p(\theta_i) = \int_{\phi_j \ge 0}^{\phi_j \le 2\pi} p(\theta_i, \phi_j) d\phi_j = \int_{\phi_j \ge 0}^{\phi_j \le 2\pi} D \ast \cos\theta_i \ast \sin\theta_i \ast d\phi_j \tag{1.20} \]

其中

\[ D_{tr\_ggx} (p, \vec{n}, \vec{h}) = \frac {\alpha^2} {\pi * ((\vec{n} \cdot \vec{h})^2 * (\alpha^2 - 1) + 1)^2} \]

展开\((1.20)\)中的D函数，得

\[ \begin{array}{l} mdf &=& p(\theta_i) = \int\limits_{\phi_j \ge 0}^{\phi_j \le 2\pi} \frac {\alpha^2} {\pi * ((\cos\theta_i)^2 * (\alpha^2 - 1) + 1)^2} \ast \cos\theta_i \ast \sin\theta_i \ast d\phi_j \\ &=& \frac {\alpha^2 \ast \cos\theta_i \ast \sin\theta_i } {\pi * ((\cos\theta_i)^2 * (\alpha^2 - 1) + 1)^2} \int\limits_{\phi_j \ge 0}^{\phi_j \le 2\pi} d\phi_j \\ &=& \frac {\alpha^2 \ast \cos\theta_i \ast \sin\theta_i } {\pi * ((\cos\theta_i)^2 * (\alpha^2 - 1) + 1)^2} \ast 2\pi \\ &=& \frac {2\alpha^2 \ast \cos\theta_i \ast \sin\theta_i } {((\cos\theta_i)^2 * (\alpha^2 - 1) + 1)^2} \end{array} \tag{1.21} \]

而对于每一个\(\phi_j\)，我们可以使用条件密度函数(conditional density function, cddf)来求得，这也是边缘分布的定义所在。

\[ cddf = p(\phi_j | \theta_i) = \frac{p(\theta_i, \phi_j)} {p(\theta_i)} \\ = \frac{D \ast \cos\theta_i \ast \sin\theta_i} {D \ast \cos\theta_i \ast \sin\theta_i \ast 2\pi} = \frac{1}{2 \pi} \tag{1.22} \]

好了，现在我们有了两个维度的pdf函数，那么接下来我们就利用反函数法来求取真正的采样点就好了。

首先，分别求出mdf和cddf的累积密度函数cdf。

\[ cdf_{mdf} = Y = P(\theta) = \int_0^{\theta} p(\theta_i) \ast d\theta_i \tag{1.23} \]

\[ cdf_{cddf} = X = P(\phi) = \int_0^{\phi} p(\phi_i | \theta_j) \ast d\phi_i \tag{1.24} \]

解\((1.23)\)和\((1.24)\)得

\[ cdf_{mdf} = Y = P(\theta) = 2 \alpha^2 \left( \frac{1}{ \left( 2 \alpha^4 - 4 \alpha^2 + 2 \right) (\cos\theta)^2 + 2 \alpha^2 - 2} - \frac{1}{2 \alpha^4 - 2 \alpha^2 } \right) \tag{1.25} \]

\[ cdf_{cddf} = X = P(\phi) = \frac{\phi}{2\pi} \tag{1.26} \]

可在如下网站验证所求积分的正确性。

mdf的cdf

cddf的cdf

然后，分别求其反函数，得

\[ \theta = P^{-1}(Y) = \cos^{-1}(\sqrt{\frac {1 - Y} {(\alpha^2 - 1) \ast Y + 1} }) \tag{1.27} \]

\[ \phi = P^{-1}(X) = 2\pi \ast X \tag{1.28} \]

至此，分布采样映射结束。好累Orz。

总结一下过程。

首先，我们通过Hammersley采样来获得N个在2D上均匀分布的采样点，设为\((x_i, y_i)\)。

然后我们求得反射率方程的概率密度函数pdf，并将其转化为极角坐标形式。

接着我们通过边缘分布对pdf进行降维打击，求得其与\(\theta\)有关的mdf函数，以及与\(\phi\)有关的cddf函数。

然后我们使用反函数法，求得mdf的累积密度函数cdf的反函数，即公式\((1.27)\)，以及cddf的累积密度函数cdf的反函数，即公式\((1.28)\)。

对于第一步求到的的\((x_i, y_i)\)，则可根据公式\((1.27)\)和公式\((1.28)\)求得\((\theta_i, \phi_i)\)。

最后再将\((\theta_i, \phi_i)\)转换到笛卡尔坐标系，得到N个半程向量\(\vec{h_i}\)。

以上过程可参考notes_on_importance_sampling理解。

代码

前文我们已经有了获取N个在2D上均匀的采样点的代码，那么从一个均匀采样点，映射到最终的重要性采样需要的采样点，即半程向量\(\vec{h_i}\)，其代码如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// 输入 -- 2D均匀分布坐标点
// 输出 -- 一个半程向量
vec3 importance_sampling_ggx(vec2 uv, float roughness, vec3 n) {
    float a = roughness * roughness;

    // 公式(1.28)求phi
    float phi = 2.0 * pi * uv.x;
    // 公式(1.27)求theta -- 只要求出其三角函数值即可
    float cos_theta = sqrt((1.0 - uv.y) / (1.0 + (a * a - 1.0) * uv.y));
    float sin_theta = sqrt(1.0 - cos_theta * cos_theta);

    // 转换成笛卡尔坐标系下的向量 -- 此时为切线空间
    vec3 h = vec3(
        sin_theta * cos(phi),
        sin_theta * sin(phi),
        cos_theta
    );

    // 坐标系转到世界坐标下 -- 乘以tbn矩阵
    vec3 up = abs(n.z) < 0.999 ? vec3(0.0, 0.0, 1.0) : vec3(1.0, 0.0, 0.0);
    vec3 right = normalize(cross(up, n));
    up = normalize(cross(n, right));

    return normalize(right * h.x + up * h.y + n * h.z);
}

然后我们便可以利用公式\((1.16)\)进行积分计算了，代码如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
vec3 pbr_ibl_specular(vec3 n, vec3 v, vec3 albedo, vec3 f0, float roughness, float metallic, uint sampler_num) {
    // 总能量值积分
    vec3 res = vec3(0.0, 0.0, 0.0);

    // 采样sampler_num个点
    for(uint i = 0u; i < sampler_num; ++i) {
        // 使用hammersley采样获得均匀分布的2D点
        vec2 uv = hammersley(i, sampler_num);

        // 重要性采样 -- 获得当前采样得到的半程向量
        vec3 h = importance_sampling_ggx(uv, roughness, n);
        // 从 v(观察方向) 和 h(半程向量) 逆算 l(光源方向)
        vec3 l = normalize(2.0 * dot(v, h) * h - v);

        // 辅助计算常用
        float n_o_v = max(dot(n, v), 0.0);
        float n_o_l = max(dot(n, l), 0.0);
        float n_o_h = max(dot(n, h), 0.0);
        float h_o_v = max(dot(h, v), 0.0);

        if(n_o_l > 0.0) {
            // 根据直接光源/IBL 选择相应方程
            float k = brdf_g_k_ibl(roughness);

            // d g f
            vec3 f90 = brdf_f_f0(f0, albedo, metallic);
            float d = brdf_d_tr_ggx(n_o_h, roughness);
            float g = brdf_g_smith(n_o_v, n_o_l, k);
            vec3  f = brdf_f_fresnel_schlick(h_o_v, f90);

            // pdf
            float pdf = d * n_o_h / (4.0 * h_o_v);

            // 采样光源方向l上的原料光强
            vec3 Li = texture(u_ibl_prefilter_map, l).xyz;

            // 代入公式(1.16)
            res += Li * f * g * h_o_v / (n_o_h * n_o_v);
        }

    }

    // 最终求的是数学期望
    res /= sampler_num;

    return res;
}

// 其中获得k值的函数与计算diffuse IBL时不同，采用下面的公式，而不是之前的Disney映射
float brdf_g_k_ibl(float roughness) { return roughness*roughness / 2.0; }

其中涉及到的未在此处展开的函数调用，在笔者之前的系列文章都可以找的到，可以往前翻看一下。

降噪

根据mipmap降噪_见20.4

经过上文所述步骤计算后，我们最终获得的渲染结果会有一些噪点，尤其是在pdf函数比较小的地方。

其原因用人话讲大概是这么个意思，就是说在pdf比较小的地方，其包含的光照信息很少，但是我们一旦确定采样那里，那么它就和pdf很高的地方对最终光强作出的贡献没什么两样了，这就会显得很突兀。

上文中提供了一种方法，根据pdf的大小来决定采样光源(一张立方体贴图)的哪一层Lod，在pdf小的地方就选择Lod级数小的，这样细节就被周围的像素点给麿掉了，就没有那么突兀了。

从pdf获得相应的Lod层数，遵循以下公式。其描述和证明在上面的链接中可以看到，这里写累了，先不解释，以后有时间了再展开。

\[ Lod = max[\frac{1}{2}log_2(\frac{\Omega_s}{\Omega_p}), 0] \\ = max[\frac{1}{2}log_2(\frac{w \ast b}{N}) - \frac{1}{2}log_2(pdf(\vec{h_i})), 0] \tag{1.29} \]

其中w和b分别是原始光源贴地的图像分辨率，N为总采样数。

其中

\[\Omega_s = \frac{1}{N \ast pdf(\vec{h_i})}\]

\[\Omega_p = \frac{4\pi}{6 \ast w \ast b}\]

代码如下。

1
2
3
4
5
6
7
8
float pbr_ibl_lod_get(float pdf, float w, float b, float sampler_num) {
    float omega_p = 4.0 * pi / (6.0 * w * b);
    float omega_s = 1.0 / (pdf * sampler_num);

    if(pdf < 0.0001) return 0.0;

    return max(0.5 * log2(omega_s / omega_p), 0.0);
}

而最终的积分过程也多了一步根据pdf获取LOD的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
vec3 pbr_ibl_specular(vec3 n, vec3 v, vec3 albedo, vec3 f0, float roughness, float metallic, uint sampler_num) {
    // 总能量值积分
    vec3 res = vec3(0.0, 0.0, 0.0);

    // 采样sampler_num个点
    for(uint i = 0u; i < sampler_num; ++i) {
        // 使用hammersley采样获得均匀分布的2D点
        vec2 uv = hammersley(i, sampler_num);

        // 重要性采样 -- 获得当前采样得到的半程向量
        vec3 h = importance_sampling_ggx(uv, roughness, n);
        // 从 v(观察方向) 和 h(半程向量) 逆算 l(光源方向)
        vec3 l = normalize(2.0 * dot(v, h) * h - v);

        // 辅助计算常用
        float n_o_v = max(dot(n, v), 0.0);
        float n_o_l = max(dot(n, l), 0.0);
        float n_o_h = max(dot(n, h), 0.0);
        float h_o_v = max(dot(h, v), 0.0);

        if(n_o_l > 0.0) {
            // 根据直接光源/IBL 选择相应方程
            float k = brdf_g_k_ibl(roughness);

            // d g f
            vec3 f90 = brdf_f_f0(f0, albedo, metallic);
            float d = brdf_d_tr_ggx(n_o_h, roughness);
            float g = brdf_g_smith(n_o_v, n_o_l, k);
            vec3  f = brdf_f_fresnel_schlick(h_o_v, f90);

            // pdf
            float pdf = d * n_o_h / (4.0 * h_o_v);
            // 获得 lod
            float lod = pbr_ibl_lod_get(pdf, 1024, 1024, sampler_num);

            // 采样光源方向l上的原料光强
            vec3 Li = textureLod(u_ibl_prefilter_map, l, lod).xyz;
            // vec3 Li = texture(u_ibl_prefilter_map, l).xyz;

            // 代入公式(1.16)
            res += Li * f * g * h_o_v / (n_o_h * n_o_v);
        }

    }

    // 最终求的是数学期望
    res /= sampler_num;

    return res;
}

运行上面的shader代码，最终后呈现的效果如下。

运行结果
大理石玻璃球不知道是啥，溜溜红球

结语

本篇描述了使用暴力手段运行时在片段着色器里计算specular IBL，其主要内容还是使用采样分布映射合理地使用采样点，然后进行积分即可。个人感觉理解难度不大，由于最近一年来比较慵懒，距离实现这部分代码已经过去一年多了，现在回想起来尝试去理解和叙述，又有了一些新的认识和体会，个人感觉这部分理解起来难度没有很大，只要不是只看开头和结果，自己跟着每一个过程和每一个公式去推导和实现，基本上没有哪一步是理解不下来的(差点Orz)。

后面还有一篇是Epic的specular IBL方案，通过将公式\((0.2)\)近似为两个可以预处理的部分，分别预处理进行，可以避免掉在片段着色器里进行积分操作。

但是个人感觉这个过程只能预处理静态的环境映射，不知道动态的是怎么处理的。。Orz。

本来打算有时间实现一下球谐光照，把反射探头做了。可以看到上面结果中每一个球体的环境光都是一样的，好像他们在同一个位置一样，这就是没有实现反射探头导致的。但是感觉后续想学的其他渲染上的东西有点多，感觉很难专门抽出时间来实现这一块，只能在这里臆想一下了。

大概看了一下球谐光照的原理，感觉和FFT(快速傅立叶变换)的原理差不多(怎么有种刷题的感觉Orz)。只不过是在球面上做FFT罢了。将频域信号通过时域信号保存下来，拟合，嗯，就这么简单，先这么骗着自己吧-_-|||。

打算更完后面Epic的预处理specular IBL，就开始研究unreal的渲染框架，先给自己定制个小目标，先看个一万行代码吧Orz。

刚才说的不算，先定制个目标清单。

理解ue4的多线程(AsyncTask和TaskGraph(主要))。

game线程、rhi线程、render线程的数据流转和协作关系。

ue4前向渲染一帧的过程。

ue4延迟渲染一帧的过程(可选)。(这两个主要是对渲染流程的把控)。

自定义渲染管线。(进行到这说明对渲染框架已经有些了解了哦-o-)。

ue4内pbr的具体实现过程。(如果上一步可以做到的话，这一步应该不难)。

使用ue4进行其他图形学知识学习和实验。(理想的终极目标Orz)

长吁一口气，感觉过去一年过的有些失败Orz，似乎少了许多曾经那种很热情地去追求某样东西的心境了，今年可不能再这样了(吧？)。

童话和现实的话，我更愿意选择相信童话\(^o^)/。